graphtraverse

Traverse graph by following adjacent nodes

Syntax

[disc, pred, closed] = graphtraverse(G, S)
[...] = graphtraverse(G, S, ...'Depth', DepthValue, ...)
[...] = graphtraverse(G, S, ...'Directed', DirectedValue, ...)
[...] = graphtraverse(G, S, ...'Method', MethodValue, ...)

Arguments

G N-by-N sparse matrix that represents a directed graph. Nonzero entries in matrix G indicate the presence of an edge.
SInteger that indicates the source node in graph G.
DepthValueInteger that indicates a node in graph G that specifies the depth of the search. Default is Inf (infinity).
DirectedValueProperty that indicates whether graph G is directed or undirected. Enter false for an undirected graph. This results in the upper triangle of the sparse matrix being ignored. Default is true.
MethodValueCharacter vector or string that specifies the algorithm used to traverse the graph. Choices are:

  • 'BFS' — Breadth-first search. Time complexity is O(N+E), where N and E are number of nodes and edges respectively.

  • 'DFS' — Default algorithm. Depth-first search. Time complexity is O(N+E), where N and E are number of nodes and edges respectively.

Description

Tip

For introductory information on graph theory functions, see Graph Theory Functions.

[disc, pred, closed] = graphtraverse(G, S) traverses graph G starting from the node indicated by integer S. G is an N-by-N sparse matrix that represents a directed graph. Nonzero entries in matrix G indicate the presence of an edge. disc is a vector of node indices in the order in which they are discovered. pred is a vector of predecessor node indices (listed in the order of the node indices) of the resulting spanning tree. closed is a vector of node indices in the order in which they are closed.

[...] = graphtraverse(G, S, ...'PropertyName', PropertyValue, ...) calls graphtraverse with optional properties that use property name/property value pairs. You can specify one or more properties in any order. Each PropertyName must be enclosed in single quotes and is case insensitive. These property name/property value pairs are as follows:

[...] = graphtraverse(G, S, ...'Depth', DepthValue, ...) specifies the depth of the search. DepthValue is an integer indicating a node in graph G. Default is Inf (infinity).

[...] = graphtraverse(G, S, ...'Directed', DirectedValue, ...) indicates whether the graph is directed or undirected. Set DirectedValue to false for an undirected graph. This results in the upper triangle of the sparse matrix being ignored. Default is true.

[...] = graphtraverse(G, S, ...'Method', MethodValue, ...) lets you specify the algorithm used to traverse the graph. Choices are:

  • 'BFS' — Breadth-first search. Time complexity is O(N+E), where N and E are number of nodes and edges respectively.

  • 'DFS' — Default algorithm. Depth-first search. Time complexity is O(N+E), where N and E are number of nodes and edges respectively.

Examples

  1. Create a directed graph with 10 nodes and 12 edges.

    DG = sparse([1 2 3 4 5 5 5 6 7 8 8 9],...
              [2 4 1 5 3 6 7 9 8 1 10 2],true,10,10)

DG =

   (3,1)        1
   (8,1)        1
   (1,2)        1
   (9,2)        1
   (5,3)        1
   (2,4)        1
   (4,5)        1
   (5,6)        1
   (5,7)        1
   (7,8)        1
   (6,9)        1
   (8,10)       1

h = view(biograph(DG))
Biograph object with 10 nodes and 12 edges.

  2. Traverse the graph to find the depth-first search (DFS) discovery order starting at node 4.

    order = graphtraverse(DG,4)

order =

     4     5     3     1     2     6     9     7     8    10

  3. Label the nodes with the DFS discovery order.

    for i = 1:10
    h.Nodes(order(i)).Label =...
			sprintf('%s:%d',h.Nodes(order(i)).ID,i);
end
h.ShowTextInNodes = 'label'
dolayout(h)

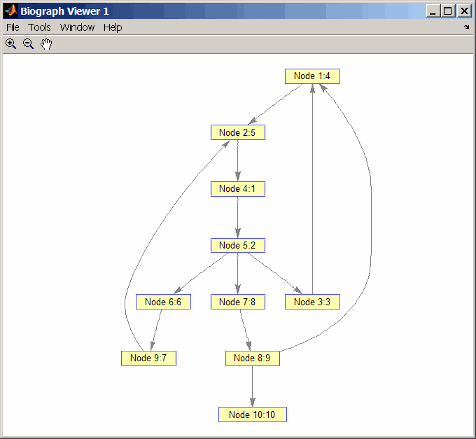
  4. Traverse the graph to find the breadth-first search (BFS) discovery order starting at node 4.

    order = graphtraverse(DG,4,'Method','BFS')

order =

     4     5     3     6     7     1     9     8     2    10

  5. Label the nodes with the BFS discovery order.

    for i = 1:10
    h.Nodes(order(i)).Label =...
			sprintf('%s:%d',h.Nodes(order(i)).ID,i);
end
h.ShowTextInNodes = 'label'
dolayout(h)

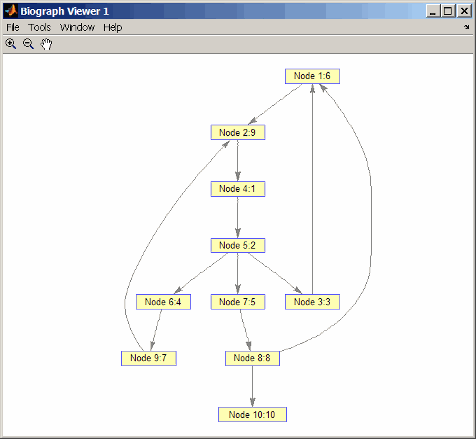
  6. Find and color nodes that are close to (within two edges of) node 4.

    node_idxs = graphtraverse(DG,4,'depth',2)

node_idxs =

     4     5     3     6     7

set(h.nodes(node_idxs),'Color',[1 0 0])

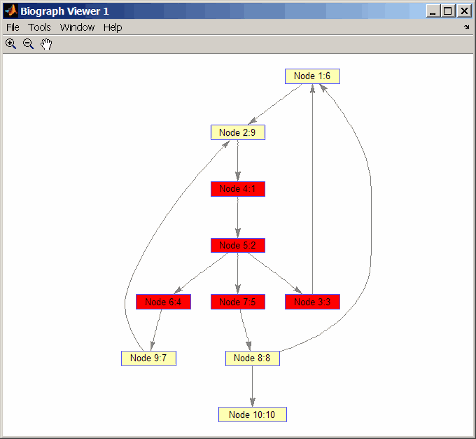
References

[1] Sedgewick, R., (2002). Algorithms in C++, Part 5 Graph Algorithms (Addison-Wesley).

[2] Siek, J.G., Lee, L-Q, and Lumsdaine, A. (2002). The Boost Graph Library User Guide and Reference Manual, (Upper Saddle River, NJ:Pearson Education).

See Also

| | | | | | | | | |

Introduced in R2006b

Bioinformatics Toolbox Documentation

Support