graphtopoorder

Perform topological sort of directed acyclic graph

Syntax

order = graphtopoorder(G)

Arguments

G N-by-N sparse matrix that represents a directed acyclic graph. Nonzero entries in matrix G indicate the presence of an edge.

Description

Tip

For introductory information on graph theory functions, see Graph Theory Functions.

order = graphtopoorder(G) returns an index vector with the order of the nodes sorted topologically. In topological order, an edge can exist between a source node u and a destination node v, if and only if u appears before v in the vector order. G is an N-by-N sparse matrix that represents a directed acyclic graph (DAG). Nonzero entries in matrix G indicate the presence of an edge.

Examples

  1. Create and view a directed acyclic graph (DAG) with six nodes and eight edges.

    DG = sparse([6 6 6 2 2 3 5 1],[2 5 1 3 4 5 1 4],true,6,6)

DG =

   (5,1)        1
   (6,1)        1
   (6,2)        1
   (2,3)        1
   (1,4)        1
   (2,4)        1
   (3,5)        1
   (6,5)        1

view(biograph(DG))

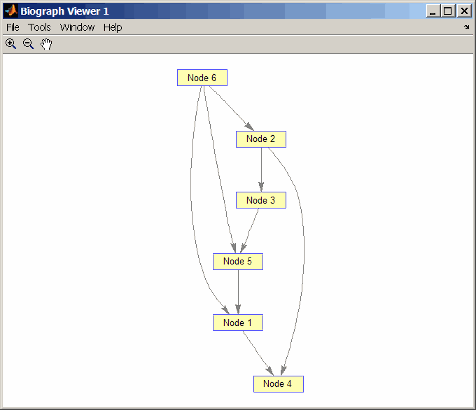
  2. Find the topological order of the DAG.

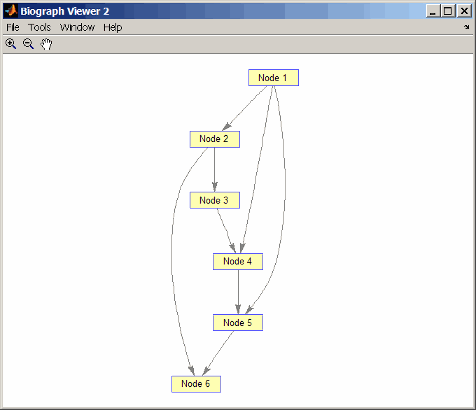
    order = graphtopoorder(DG)

order =

     6     2     3     5     1     4

  3. Permute the nodes so that they appear ordered in the graph display.

    DG = DG(order,order)

DG =

   (1,2)        1
   (2,3)        1
   (1,4)        1
   (3,4)        1
   (1,5)        1
   (4,5)        1
   (2,6)        1
   (5,6)        1

view(biograph(DG))

References

[1] Siek, J.G., Lee, L-Q, and Lumsdaine, A. (2002). The Boost Graph Library User Guide and Reference Manual, (Upper Saddle River, NJ:Pearson Education).

See Also

| | | | | | | | | |

Introduced in R2006b

Bioinformatics Toolbox Documentation

Support