patch

Plot one or more filled polygonal regions

collapse all in page

Syntax

patch(X,Y,C)
patch(X,Y,Z,C)
patch('XData',X,'YData',Y)
patch('XData',X,'YData',Y,'ZData',Z)
patch('Faces',F,'Vertices',V)
patch(S)
patch(___,Name,Value)
patch(ax,___)
p = patch(___)

Description

example

patch(X,Y,C) plots one or more filled polygonal regions using the elements of X and Y as the coordinates for each vertex. patch connects the vertices in the order that you specify them. To create one polygon, specify X and Y as vectors. To create multiple polygons, specify X and Y as matrices where each column corresponds to a polygon. C determines the polygon colors.

patch(X,Y,Z,C) creates the polygons in 3-D coordinates using X, Y, and Z. To view the polygons in a 3-D view, use the view(3) command. C determines the polygon colors.

patch('XData',X,'YData',Y) is similar to patch(X,Y,C), except that you do not have to specify color data for the 2-D coordinates.

patch('XData',X,'YData',Y,'ZData',Z) is similar to patch(X,Y,Z,C), except that you do not have to specify color data for the 3-D coordinates.

example

patch('Faces',F,'Vertices',V) creates one or more polygons where V specifies vertex values and F defines which vertices to connect. Specifying only unique vertices and their connection matrix can reduce the size of the data when there are many polygons. Specify one vertex per row in V. To create one polygon, specify F as a vector. To create multiple polygons, specify F as a matrix with one row per polygon. Each face does not have to have the same number of vertices. To specify different numbers of vertices, pad F with NaN values.

example

patch(S) creates one or more polygons using structure S. The structure fields correspond to patch property names and the field values corresponding to property values. For example, S can contain the fields Faces and Vertices.

example

patch(___,Name,Value) creates polygons and specifies one or more patch properties using name-value pair arguments. A patch is the object that contains the data for all of the polygons created. You can specify patch properties with any of the input argument combinations in the previous syntaxes. For example, 'LineWidth',2 sets the outline width for all of the polygons to 2 points.

patch(ax,___) creates the patch in the axes specified by ax instead of in the current axes (gca). The option ax can precede any of the input argument combinations in the previous syntaxes.

p = patch(___) returns the patch object that contains the data for all the polygons. Use p to query and modify properties of the patch object after it is created. For a list of properties and descriptions, see Patch Properties.

Examples

collapse all

Open Live Script

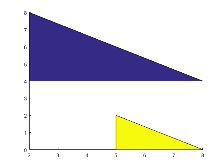
Create a single polygon by specifying the (x,y) coordinates of each vertex. Then, add two more polygons to the figure.

Create a red square with vertices at (0,0), (1,0), (1,1), and (0,1). Specify x as the x-coordinates of the vertices and y as the y-coordinates. patch automatically connects the last (x,y) coordinate with the first (x,y) coordinate.

x = [0 1 1 0];
y = [0 0 1 1];
patch(x,y,'red')

Create two polygons by specifying x and y as two-column matrices. Each column defines the coordinates for one of the polygons. patch adds the polygons to the current axes without clearing the axes.

x2 = [2 5; 2 5; 8 8];
y2 = [4 0; 8 2; 4 0];
patch(x2,y2,'green')

Open Live Script

Create a single polygon by specifying the coordinates of each unique vertex and a matrix that defines how to connect them. Then, add two more polygons to the figure.

Create a red square with corners at (0,0), (1,0), (1,1), and (0,1). Specify v so that each row defines the (x,y) coordinates for one vertex. Then, specify f as the vertices to connect. Set the color by specifying the FaceColor property.

v = [0 0; 1 0; 1 1; 0 1];
f = [1 2 3 4];
patch('Faces',f,'Vertices',v,'FaceColor','red')

Create two polygons by specifying f as a two-row matrix. Each row defines the face for one patch.

v2 = [2 4; 2 8; 8 4; 5 0; 5 2; 8 0];
f2 = [1 2 3; 
    4 5 6];
patch('Faces',f2,'Vertices',v2,'FaceColor','green')

Open Live Script

Create two polygons and use a different color for each polygon face. Use a colorbar to show how the colors map into the colormap.

Create the polygons using matrices x and y. Specify c as an column vector with two elements since there are two polygon faces, and add a colorbar.

x = [2 5; 2 5; 8 8];
y = [4 0; 8 2; 4 0];
c = [0; 1];
figure
patch(x,y,c)
colorbar

Alternatively, you can get the same result when using f and v instead. When you create the polygons, set FaceVertexCData to a column vector with two elements since there are two polygon faces. Set FaceColor to 'flat'.

v = [2 4; 2 8; 8 4; 5 0; 5 2; 8 0];
f = [1 2 3; 4 5 6];
col = [0; 1];
figure
patch('Faces',f,'Vertices',v,'FaceVertexCData',col,'FaceColor','flat');
colorbar

Open Live Script

Interpolate colors across polygon faces by specifying a color at each polygon vertex, and use a colorbar to show how the colors map into the colormap.

Create the polygons using matrices x and y. Specify c as a matrix the same size as x and y defining one color per vertex, and add a colorbar.

x = [2 5; 2 5; 8 8];
y = [4 0; 8 2; 4 0];
c = [0 3; 6 4; 4 6];
figure
patch(x,y,c)
colorbar

Alternatively, you can get the same result using f and v instead. When you create the polygons, set FaceVertexCData to a column vector with one value per vertex and set FaceColor to 'interp'.

v = [2 4; 2 8; 8 4; 5 0; 5 2; 8 0];
f = [1 2 3; 4 5 6];
col = [0; 6; 4; 3; 4; 6];
figure
patch('Faces',f,'Vertices',v,'FaceVertexCData',col,'FaceColor','interp');
colorbar

Open Live Script

Create a polygon with green edges and do not display the face. Then, create a second polygon with a different color for each edge.

v = [0 0; 1 0; 1 1];
f = [1 2 3];
figure
patch('Faces',f,'Vertices',v,...
    'EdgeColor','green','FaceColor','none','LineWidth',2);

Use a different color for each edge by specifying a color for each vertex and setting EdgeColor to 'flat'. 

v = [2 0; 3 0; 3 1];
f = [1 2 3];
c = [1 0 0; % red
    0 1 0; % green
    0 0 1]; % blue
patch('Faces',f,'Vertices',v,'FaceVertexCData',c,...
    'EdgeColor','flat','FaceColor','none','LineWidth',2);

Open Live Script

Use a structure to create two polygons. First, create a structure with fields names that match patch property names. Then, use the structure to create the polygons.

clear S
S.Vertices = [2 4; 2 8; 8 4; 5 0; 5 2; 8 0];
S.Faces = [1 2 3; 4 5 6];
S.FaceVertexCData = [0; 1];
S.FaceColor = 'flat';
S.EdgeColor = 'red';
S.LineWidth = 2;
figure
patch(S)

Open Live Script

Create two semitransparent polygons by setting the FaceAlpha property to a value between 0 and 1.

v1 = [2 4; 2 8; 8 4];
f1 = [1 2 3];
figure
patch('Faces',f1,'Vertices',v1,'FaceColor','red','FaceAlpha',.3);

v2 = [2 4; 2 8; 8 8];
f2 = [1 2 3];
patch('Faces',f2,'Vertices',v2,'FaceColor','blue','FaceAlpha',.5);

Open Live Script

Create a multicolored line with markers at each vertex. Interpolate the colors and use a colorbar to show how the values map to the colormap.

Create the data. Set the last entry of y to NaN so that patch creates a line instead of a closed polygon. Define a color for each vertex using the y values. The values in c map to colors in the colormap. 

x = linspace(1,10,15);
y = sin(x);
y(end) = NaN;
c = y;

Create the line. Show markers at each vertex and set the EdgeColor to 'interp' to interpolate the colors between vertices. Add a colorbar.

figure
patch(x,y,c,'EdgeColor','interp','Marker','o','MarkerFaceColor','flat');
colorbar;

Input Arguments

collapse all

x-coordinates for the vertices, specified in one of these forms:

  • Vector — Create one polygon.

  • Matrix — Create n polygons with m vertices each, where [m,n] = size(X). Each column in the matrix corresponds to one polygon.

If the data does not define closed polygons, then patch closes the polygons. If the edges of an individual polygon intersect themselves, the resulting polygons might be partly filled. In that case, it is better to divide the patch object into smaller polygons.

When you specify X, the patch function sets the XData property for the patch object to the same value. The patch object automatically calculates the face and vertex data and sets the Faces and Vertices properties to the appropriate values.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

y-coordinates for the vertices, specified in one of these forms:

  • Vector — Create one polygon.

  • Matrix — Create n polygons with m vertices each, where [m,n] = size(Y). Each column in the matrix corresponds to one polygon.

If the data does not define closed polygons, then patch closes the polygons. If the edges of an individual polygon intersect themselves, the resulting polygons might be partly filled. In that case, it is better to divide the patch object into smaller polygons.

When you specify Y, the patch function sets the YData property for the patch object to the same value. The patch object automatically calculates the face and vertex data and sets the Faces and Vertices properties to the appropriate values.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

z-coordinates for the vertices, specified in one of these forms:

  • Vector — Create one polygon.

  • Matrix — Create m polygons with n vertices each, where [m,n] = size(Z). Each column in the matrix corresponds to one polygon.

When you specify Z, the patch function sets the ZData property for the patch object to the same value. The patch object automatically calculates the face and vertex data and sets the Faces and Vertices properties to the appropriate values.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

Polygon colors, specified as a scalar, vector, matrix, or a color name. The format of the input determines whether all polygons have the same color, one color per face, or interpolated face colors.

Desired EffectUse One of These FormatsResults
Single color for all faces

  • Color name, for example, 'r' for red.

  • RGB triplet, for example, [0 .5 .5].

  • Scalar value, for example, 2. The CDataMapping property determines how the value maps into the colormap.

For an example, see Specifying Coordinates.

  • Sets the FaceColor property to the specified color.

One color per face

  • n-by-1 vector of colormap colors, where n is the number of faces. The CDataMapping property determines how the values map into the colormap.

  • n-by-1-by-3 array of RGB values. The first page of the array defines the red components of the colors, the second page defines the blue, and the third page defines the green.

For an example, see Different Polygon Face Colors.

Interpolated face colors

  • m-by-n matrix of colormap values, where [m,n] = size(X). Specify one color per vertex.

  • m-by-n-by-3 array of RGB values.

For an example, see Interpolated Polygon Face Colors.

An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range [0,1]; for example, [0.4 0.6 0.7]. Alternatively, you can specify some common colors by name. This table lists the long and short color name options and the equivalent RGB triplet values.

OptionDescriptionEquivalent RGB Triplet
'red' or 'r'Red[1 0 0]
'green' or 'g'Green[0 1 0]
'blue' or 'b'Blue[0 0 1]
'yellow' or 'y'Yellow[1 1 0]
'magenta' or 'm'Magenta[1 0 1]
'cyan' or 'c'Cyan[0 1 1]
'white' or 'w'White[1 1 1]
'black' or 'k'Black[0 0 0]

Polygon vertices, specified in one of these forms:

  • Two-column matrix — Each row contains the (x,y) coordinates for a vertex.

  • Three-column matrix — Each row contains the (x,y,Z) coordinates for a vertex.

Specify only unique vertices. You can refer to a vertex more than once when defining the face definitions in F.

When you specify V, the patch function sets the Vertices property for the patch object to the same value. The patch object automatically calculates the coordinate data and sets the XData, YData, and ZData to the appropriate values.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

Face definitions, specified in one of these forms:

  • Row vector — Create a single polygon.

  • Matrix — Create multiple polygons where each row corresponds to a polygon.

For example, this code defines three vertices in V and creates one polygon by connecting vertex 1 to 2, 2 to 3, and 3 to 1.

V = [1 1; 2 1; 2 2];
F = [1 2 3 1];
patch('Faces',F,'Vertices',V)

When you specify F, the patch function sets the Faces property for the patch object to the same value. The patch object automatically calculates the coordinate data and sets the XData, YData, and ZData to the appropriate values.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

Patch definition, specified as a structure with fields that correspond patch property names and field values that correspond to patch property values.

Axes object. If you do not specify an axes object, then patch uses the current axes.

Name-Value Pair Arguments

Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside quotes. You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

Example: patch(x,y,c,'FaceAlpha',.5,'LineStyle',':') creates semitransparent polygons with dotted edges.

The properties listed here are only a subset of patch properties. For a complete list, see Patch Properties.

Face color, specified as 'interp', 'flat' an RGB triplet, a hexadecimal color code, a color name, or a short name.

To create a different color for each face, specify the CData or FaceVertexCData property as an array containing one color per face or one color per vertex. The colors can be interpolated from the colors of the surrounding vertices of each face, or they can be uniform. For interpolated colors, specify this property as 'interp'. For uniform colors, specify this property as 'flat'. If you specify 'flat' and a different color for each vertex, the color of the first vertex you specify determines the face color.

To designate a single color for all of the faces, specify this property as an RGB triplet, a hexadecimal color code, a color name, or a short name.

  • An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range [0,1]; for example, [0.4 0.6 0.7].

  • A hexadecimal color code is a character vector or a string scalar that starts with a hash symbol (#) followed by three or six hexadecimal digits, which can range from 0 to F. The values are not case sensitive. Thus, the color codes '#FF8800', '#ff8800', '#F80', and '#f80' are equivalent.

Color NameShort NameRGB TripletHexadecimal Color CodeAppearance
'red''r'[1 0 0]'#FF0000'

'green''g'[0 1 0]'#00FF00'

'blue''b'[0 0 1]'#0000FF'

'cyan' 'c'[0 1 1]'#00FFFF'

'magenta''m'[1 0 1]'#FF00FF'

'yellow''y'[1 1 0]'#FFFF00'

'black''k'[0 0 0]'#000000'

'white''w'[1 1 1]'#FFFFFF'

'none'Not applicableNot applicableNot applicableNo color

Here are the RGB triplets and hexadecimal color codes for the default colors MATLAB® uses in many types of plots.

RGB TripletHexadecimal Color CodeAppearance
[0 0.4470 0.7410]'#0072BD'

[0.8500 0.3250 0.0980]'#D95319'

[0.9290 0.6940 0.1250]'#EDB120'

[0.4940 0.1840 0.5560]'#7E2F8E'

[0.4660 0.6740 0.1880]'#77AC30'

[0.3010 0.7450 0.9330]'#4DBEEE'

[0.6350 0.0780 0.1840]'#A2142F'

Face transparency, specified as one of these values:

  • Scalar in range [0,1] — Use uniform transparency across all of the faces. A value of 1 is fully opaque and 0 is completely transparent. This option does not use the transparency values in the FaceVertexAlphaData property.

  • 'flat' — Use a different transparency for each face based on the values in the FaceVertexAlphaData property. First you must specify the FaceVertexAlphaData property as a vector containing one transparency value per face or vertex. The transparency value at the first vertex determines the transparency for the entire face.

  • 'interp' — Use interpolated transparency for each face based on the values in FaceVertexAlphaData property. First you must specify the FaceVertexAlphaData property as a vector containing one transparency value per vertex. The transparency varies across each face by interpolating the values at the vertices.

Edge colors, specified as one of the values in this table. The default edge color is black with a value of [0 0 0]. If multiple polygons share an edge, then the first polygon drawn controls the displayed edge color.

ValueDescriptionResult

RGB triplet, hexadecimal color code, or color name

Single color for all of the edges. See the following table for more details.

'flat'

Different color for each edge. Use the vertex colors to set the color of the edge that follows it. You must first specify CData or FaceVertexCData as an array containing one color per vertex. The edge color depends on the order in which you specify the vertices.

'interp'

Interpolated edge color. You must first specify CData or FaceVertexCData as an array containing one color per vertex. Determine the edge color by linearly interpolating the values at the two bounding vertices.

'none'No edges displayed.

No edges displayed.

RGB triplets and hexadecimal color codes are useful for specifying custom colors.

  • An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range [0,1]; for example, [0.4 0.6 0.7].

  • A hexadecimal color code is a character vector or a string scalar that starts with a hash symbol (#) followed by three or six hexadecimal digits, which can range from 0 to F. The values are not case sensitive. Thus, the color codes '#FF8800', '#ff8800', '#F80', and '#f80' are equivalent.

Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and hexadecimal color codes.

Color NameShort NameRGB TripletHexadecimal Color CodeAppearance
'red''r'[1 0 0]'#FF0000'

'green''g'[0 1 0]'#00FF00'

'blue''b'[0 0 1]'#0000FF'

'cyan' 'c'[0 1 1]'#00FFFF'

'magenta''m'[1 0 1]'#FF00FF'

'yellow''y'[1 1 0]'#FFFF00'

'black''k'[0 0 0]'#000000'

'white''w'[1 1 1]'#FFFFFF'

Here are the RGB triplets and hexadecimal color codes for the default colors MATLAB uses in many types of plots.

RGB TripletHexadecimal Color CodeAppearance
[0 0.4470 0.7410]'#0072BD'

[0.8500 0.3250 0.0980]'#D95319'

[0.9290 0.6940 0.1250]'#EDB120'

[0.4940 0.1840 0.5560]'#7E2F8E'

[0.4660 0.6740 0.1880]'#77AC30'

[0.3010 0.7450 0.9330]'#4DBEEE'

[0.6350 0.0780 0.1840]'#A2142F'

Line style, specified as one of the options listed in this table.

Line StyleDescriptionResulting Line
'-'Solid line

'--'Dashed line

':'Dotted line

'-.'Dash-dotted line

'none'No lineNo line

Output Arguments

collapse all

Patch object, returned as a scalar. Each patch object can consist of one or more polygons. Use p to query or change properties of the patch object after it is created.

Extended Capabilities

See Also

Functions

Properties

Topics

Introduced before R2006a

MATLAB Documentation

Support