Synchronous Machine

Description

The Synchronous Machine block operates in generator or motor modes. The operating mode is dictated by the sign of the mechanical power (positive for generator mode, negative for motor mode). The electrical part of the machine is represented by a sixth-order state-space model and the mechanical part is the same as in the Simplified Synchronous Machine block.

The model takes into account the dynamics of the stator, field, and damper windings. The equivalent circuit of the model is represented in the rotor reference frame (qd frame). All rotor parameters and electrical quantities are viewed from the stator. They are identified by primed variables. The subscripts are:

d,q — d- and q-axis quantity
R,s — Rotor and stator quantity
l,m — Leakage and magnetizing inductance
f,k — Field and damper winding quantity

The electrical model of the machine is shown in these diagrams.

Dynamic Model with Unequal Mutual Inductance

The conventional theory of the Synchronous Machine modeling for stability analysis assumes that the mutual inductances between the armature, damper, and field on direct-axis windings are identical. Generally, damper windings are near the air gap, and as a result the flux linking damper circuits is almost equal to flux linking armature. This hypothesis produces acceptable outcomes for a wide range of stability studies, especially those of the networkside. However, when it comes to field current studies, there is a considerable error. The equivalent circuit dynamic model of synchronous machine may include an additional inductance representing the difference between field-damper and field-armature mutual inductances on D-axis [1]. This inductance is typically called Canay inductance. Canay inductance corresponds to the leakage flux, Φ_C, in the following figure and is interpreted as a corrective element in an equivalent model that may have a negative value [2].

The IEEE standard 1110-2002 [3] presents the direct and quadratic axes of synchronous machine dynamic model as shown in the diagrams.

The relevant equations are:

$\begin{array}{l} V_{d} = - i_{d} R_{s} - ω ψ_{q} + \frac{d ψ_{d}}{d t} \\ V_{q} = - i_{q} R_{s} + ω ψ_{d} + \frac{d ψ_{q}}{d t} \\ V_{0} = - i_{0} R_{0} + \frac{d ψ_{0}}{d t} \\ V_{f d} = \frac{d ψ_{f d}}{d t} + R_{f d} i_{f d} \\ 0 = \frac{d ψ_{k d}}{d t} + R_{k d} i_{k d} \\ 0 = \frac{d ψ_{k q 1}}{d t} + R_{k q 1} i_{k q 1} \\ 0 = \frac{d ψ_{k q 2}}{d t} + R_{k q 2} i_{k q 2} \\ [\begin{matrix} ψ_{d} \\ ψ_{k d} \\ ψ_{f d} \end{matrix}] = [\begin{matrix} L {}_{m d}+ L_{l} & L_{m d} & L_{m d} \\ L_{m d} & L_{l k d} + L_{f}_{1 d} + L_{m d} & L_{f}_{1 d} + L_{m d} \\ L_{m d} & L_{f}_{1 d} + L_{m d} & L_{l f d} + L_{f}_{1 d} + L_{m d} \end{matrix}] [\begin{matrix} - i_{d} \\ i_{k d} \\ i_{f d} \end{matrix}] \\ [\begin{matrix} ψ_{q} \\ \begin{array}{l} ψ_{k q 1} \\ ψ_{k q 2} \end{array} \end{matrix}] = [\begin{matrix} L_{m q} + L_{l} & L_{m q} & L_{m q} \\ L_{m q} & L_{m q} + L_{k q 1} & L_{m q} \\ L_{m q} & L_{m q} & L_{m q} + L_{k q 2} \end{matrix}] [\begin{array}{l} \begin{matrix} - i_{q} \\ i_{k q 1} \end{matrix} \\ i_{k q 2} \end{array}] \end{array}$

Base Values, Transformation Ratio, and Rotor Parameters Referred to the Stator

The Synchronous Machine SI Fundamental block and the Synchronous Machine pu Fundamental block allow you to specify the fundamental parameters of a synchronous machine. You enter field and damper windings parameters (resistances, leakage inductances, and mutual inductances) in SI (Ω, H) or in pu. When you enter parameters in SI, the RL parameters of field and damper windings are not the actual field RL values of the machine but the RL values referred to the stator.

You can compute base values for stator and rotor windings when the parameters are specified in pu. You can also compute the Stator/Field transformation ratio and the field parameters referred to the stator from the actual field parameters (windings RL values, nominal field voltage, and nominal field current).

Stator Base Values

This table displays stator base values.

$V_{s b a s e} = {\frac{V_{n} \sqrt{2}}{\sqrt{3}}}_{}$	Base stator voltage = peak nominal line-to-neutral voltage (V)
$I_{s b a s e} = {\frac{P_{n} \sqrt{2}}{V_{n} \sqrt{3}}}_{}$	Base stator current (A)
$Z_{s b a s e} = {\frac{V_{s b a s e}}{I_{s b a s e}}}_{} = \frac{V_{n}^{2}}{P_{n}}$	Base stator impedance (Ω)
$ω_{b a s e} = 2 π f_{n}$	Base angular frequency (rad/s)
$L_{s b a s e} = {\frac{Z_{s b a s e}}{ω_{b a s e}}}_{}$	Base stator inductance (H)

Where:

P_n = three-phase nominal power (VA)
V_n = nominal line-to-line voltage (Vrms)
f_n = nominal frequency (Hz)
i_fn = nominal field current producing nominal stator voltage at no load (A)

The stator parameters to specify in the Synchronous Machine SI Fundamental block are:

R_s = stator resistance per phase (Ω)
L_l = stator leakage inductance (H)
L_md = direct-axis magnetizing inductance viewed from stator (H)
L_mq = quadrature-axis magnetizing inductance viewed from stator (H)

The stator parameters to enter in the Synchronous Machine pu Fundamental block are:

$R_{s_p u} = \frac{R_{s}}{Z_{s b a s e}}$	Stator resistance per phase (pu)
$L_{l_p u} = \frac{L_{l}}{L_{s b a s e}}$	Stator leakage inductance (pu)
$L_{m d_p u} = \frac{L_{m d}}{L_{s b a s e}}$	Direct-axis magnetizing inductance (pu)
$L_{m q_p u} = \frac{L_{m q}}{L_{s b a s e}}$	Quadrature-axis magnetizing inductance (pu)

Stator/Field Transformation Ratio

This figure shows one phase of the stator winding coupled with the field winding.

In the diagram:

N_s and N_f are the equivalent number of sinusoidally distributed turns of the stator winding and of the field winding, respectively.
R_s and L_l are stator resistance and leakage inductance.
R_f′ and L_lfd′ are field resistance and leakage inductance.

When the three stator windings are energized with a three-phase positive-sequence voltage and field winding is open, the stator magnetizing inductance is L_md. However, when only one phase is energized and field winding is open, the magnetizing inductance is 2/3 L_md, as shown in the figure.

At no load, when the field winding is rotating at nominal speed and bears the nominal field DC current i_fn, the amplitude of AC voltage (peak value) induced on one phase of stator is V_sbase.

The maximum mutual inductance between one stator winding and the field winding is obtained when the two windings are aligned. It is given by:

$L_{s f d} = \frac{2}{3} L_{m d} \frac{N_{f}}{N_{s}} = \frac{V_{s b a s e}}{i_{f n} ω_{b a s e}}$

from which we deduce the transformation ratio:

$\frac{N_{s}}{N_{f}} = \frac{2}{3} L_{m d} \frac{i_{f n} ω_{b a s e}}{V_{s b a s e}}$

The transformation ratio can be also expressed as:

$\frac{N_{s}}{N_{f}} = \frac{2}{3} \frac{I_{f b a s e}}{I_{s b a s e}}$

where I_fbase is the base field current. The table shows how to compute field base values.

Field Base Values

This table displays field base values.

$I_{f b a s e} = i_{f n} L_{m d_p u}_{}$	Base field current (A)
$V_{f b a s e} = {\frac{P_{n}}{I_{f b a s e}}}_{}$	Base field voltage (V)
$Z_{f b a s e} = {\frac{V_{f b a s e}}{I_{f b a s e}}}_{}$	Base field impedance (Ω)
$L_{f b a s e} = {\frac{Z_{f b a s e}}{ω_{b a s e}}}_{}$	Base field inductance (H)

The actual field parameters are:

R_f′ is field resistance (Ω)

L_lfd′ is field leakage inductance (H)

The field parameters to enter in the Synchronous Machine pu Fundamental block menu are:

$R_{f_p u} = \frac{R_{f}'}{Z_{f b a s e}}$

Field resistance (pu)

$L_{l f d_p u} = \frac{L_{l}_{f d}'}{L_{f b a s e}}$

Field leakage inductance (pu)

Field Voltage, Current, and RL Values Referred to the Stator

The field parameters to enter in the Synchronous Machine SI Fundamental block are the field resistance and leakage inductance referred to the stator (R_f, L_lfd).

If the nominal field current i_fn is known, the transformation ratio N_s/N_f is calculated using the same equation as for the stator/field transformation ratio.

According to Krause [4], the field voltage and current referred to the stator (V_f, I_f) are deduced from actual V_f′ , I_f′ values as follows:

$V_{f} = \frac{N_{s}}{N_{f}} V_{f}'$

$I_{f} = \frac{2}{3} \frac{N_{f}}{N_{s}} I_{f}'$

When the actual field resistance R_f′ and leakage inductances L_lfd′ (seen from the rotor) are known, the values referred to the stator are:

$R_{f} = \frac{3}{2} R_{f}' {(\frac{N_{s}}{N_{f}})}^{2}$

$L_{l f d} = \frac{3}{2} L_{l f d}' {(\frac{N_{s}}{N_{f}})}^{2}$

When the nominal field current is not known, and if the pu values of field resistance and leakage inductances are known (R_{f_pu}, L_{lfd_pu}), the corresponding SI values referred to the stator are computed as follows:

$R_{f} = R_{f_p u} \times Z_{s b a s e}$

$L_{l f d} = L_{l f d_p u} \times L_{s b a s e}$

The same conversions are used for RL parameters of damper windings.

Field Voltage and Current for SI Fundamental Synchronous Machine

When you specify the nominal field current, the signal applied to the Vf input corresponds to the actual field voltage, as in real life. The field current returned by the measurement output also corresponds to the actual field current If.

Nominal field voltage producing nominal stator voltage at no load is given by:

$e_{f n} = R_{f}' \times i_{f n}$

When you do not specify the nominal field current, the signal applied to the Vf input corresponds to the actual field voltage referred to the stator. In this case, the nominal field voltage referred to the stator producing nominal stator voltage at no load is:

$e_{f n} (s t a t o r s i d e) = \frac{R_{f_p u}}{L_{m d_p u}} V_{s b a s e} = \frac{R_{f}}{L_{m d} ω_{b a s e}} V_{s b a s e}$

The field current returned by the measurement output is the field current referred to the stator. The nominal field current referred to the stator is:

$i_{f n} (s t a t o r s i d e) = \frac{I_{s b a s e}}{L_{m d_p u}} = \frac{I_{s b a s e}}{I_{f b a s e}} i_{f n}$

Field Voltage and Current for PU Fundamental Synchronous Machine

The voltage applied at the Vf input of the Synchronous Machine pu Fundamental block is normalized with respect to nominal field voltage so that a 1 pu input produces a 1 pu stator voltage at no load. The If current returned by the measurement output of the block is also normalized with respect to nominal field current so that a 1 pu input produces If = 1 pu.

Parameters

Depending on data availability, you can select one of three Synchronous Machine blocks from the Simscape™ Electrical™ Specialized Power Systems library (powerlib):

Synchronous Machine SI Fundamental block — Specify stator, field, and damper windings fundamental parameters (resistances, leakage inductances, and mutual inductances) in SI (Ω and H). When you enter parameters in SI, the RL parameters of field and damper windings are not the actual field RL values of the machine but the RL values referred to the stator.
Synchronous Machine pu Fundamental block — Specify fundamental parameters in pu both for the stator and rotor side.
Synchronous Machine pu Standard block — Specify standard parameters, also known as operational parameters, of the synchronous machine (steady-state, transient, and/or subtransient reactances and time constants) as input to the block. Typically, machine manufacturers provide operational parameters.

In power system analysis software, the synchronous machine equations are commonly solved using the direct-quadrature-zero transformation technique. To facilitate calculation, consider using normalized pu parameters. For the Synchronous Machine pu Fundamental block, the given data is transferred directly to the process of solving equations. In the case of the Synchronous Machine SI Fundamental block, the rotor side parameters are transferred to stator side and normalized before entering the final processing. When you select the Synchronous Machine pu Standard block, a data translation technique is required to calculate fundamental parameters from standard parameters [2], [3]. The data translation technique can translate fundamental parameters to operational parameters and vice versa.

Configuration

Preset model

Provides a set of predetermined electrical and mechanical parameters for various synchronous machine ratings of power (kVA), phase-to-phase voltage (V), frequency (Hz), and rated speed (rpm).

Select one of the preset models to load the corresponding electrical and mechanical parameters in the entries of the dialog box. Select No (default) if you do not want to use a preset model, or if you want to modify some of the parameters of a preset model, as described below.

When you select a preset model, the electrical and mechanical parameters in the Parameters tab of the dialog box become nonmodifiable (unavailable). To start from a given preset model and then modify machine parameters:

Select the preset model that you want to initialize the parameters.
Change the Preset model parameter value to No. This action does not change the machine parameters. By doing so, you just break the connection with the particular preset model.
Modify the machine parameters as you want, then click Apply.

Mechanical input

Allows you to select the mechanical power applied to the shaft or the rotor speed as a Simulink^® input of the block, or to represent the machine shaft by a Simscape rotational mechanical port.

Select Mechanical power Pm (default) to specify a mechanical power input, in W or in pu, and change labeling of the block input to Pm. The machine speed is determined by machine inertia J (or inertia constant H for the pu machine) and by the difference between the mechanical torque Tm, resulting from the applied mechanical power Pm, and the internal electromagnetic torque Te. The sign convention for the mechanical power is when the speed is positive, a positive mechanical power signal indicates generator mode and a negative signal indicates motor mode.

Select Speed w to specify a speed input, in rad/s or in pu, and change labeling of the block input to w. The machine speed is imposed and the mechanical part of the model (inertia constant H) is ignored. Using the speed as the mechanical input allows modeling a mechanical coupling between two machines.

The next figure indicates how to model a stiff shaft interconnection in a motor-generator set, where both machines are synchronous machines.

The speed output of machine 1 (motor) is connected to the speed input of machine 2 (generator). In this figure, friction torque is ignored in machine 2. Therefore, its electromagnetic torque output Te corresponds to the mechanical torque Tm applied to the shaft of machine 1. The corresponding mechanical input power of machine 1 is computed as Pm = Tm*w.The Kw factor takes into account speed units of both machines (pu or rad/s) and gear box ratio w2/w1. The KT factor takes into account torque units of both machines (pu or N.m) and machine ratings. Also, as inertia J2 is ignored in machine 2, J2 referred to machine 1 speed must be added to machine 1 inertia J1.

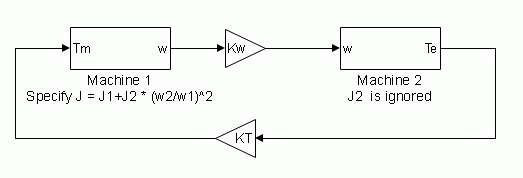
Select Mechanical rotational port to add to the block a Simscape mechanical rotational port that allows connection of the machine shaft with another machine shaft or with other Simscape blocks having mechanical rotational ports. The Simulink input representing the mechanical power Pm or the speed w of the machine is then removed from the block.

The next figure indicates how to connect an Ideal Torque Source block from the Simscape library to the machine shaft to represent the machine in motor mode, or in generator mode, when the rotor speed is positive.

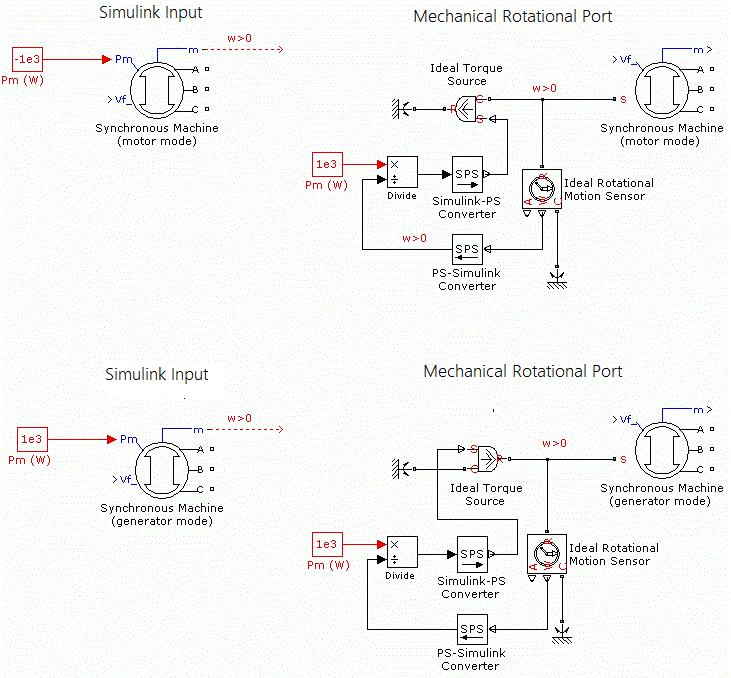
Rotor type

Specify rotor type: Salient-pole (default) or Round (cylindrical). This choice affects the number of rotor circuits in the q-axis (damper windings).

Use signal names to identify bus labels

When this check box is selected, the measurement output uses the signal names to identify the bus labels. Select this option for applications that require bus signal labels to have only alphanumeric characters.

When this check box is cleared (default), the measurement output uses the signal definition to identify the bus labels. The labels contain nonalphanumeric characters that are incompatible with some Simulink applications.

Parameters for Synchronous Machine SI Fundamental

Nominal power, voltage, frequency, field current

The total three-phase apparent power Pn (VA), RMS line-to-line voltage Vn (V), frequency fn (Hz), and field current ifn (A). Default is [ 187E6 13800 60 1087 ].

The nominal field current is the current that produces nominal terminal voltage under no-load conditions. This model was developed with all quantities viewed from the stator, as explained in Krause [4]. The nominal field current makes it possible to compute the transformation ratio of the machine, which allows you to apply the field voltage viewed from the rotor, as in real life. It also allows the field current, which is a variable in the output vector of the model, to be viewed from the rotor.

If the value of the nominal field current is not known, you must enter 0 or leave it blank. Since the transformation ratio cannot be determined in this case, you have to apply the field voltage as viewed from the stator. The field current in the output vector is also viewed from the stator.

Stator

Resistance Rs (Ω), leakage inductance Lls (H), and d-axis and q-axis magnetizing inductances Lmd (H) and Lmq (H), and Canay inductance. If the value of the Canay inductance in not known, you must enter 0 or leave it blank. Default is [ 2.9069E-03 3.0892E-04 3.2164E-03 9.7153E-04 ].

Field

Field resistance Rf (Ω) and leakage inductance Llfd (H), both referred to the stator. Default is [ 5.9013E-04 3.0712E-04 ].

Dampers

The d-axis resistance Rkd (Ω) and leakage inductance Llkd (H), the q-axis resistance Rkq1 (Ω) and leakage inductance Llkq1 (H), and (only if round rotor) the q-axis resistance Rkq2 (Ω) and leakage inductance Llkq2 (H). All of these values are referred to the stator. Default is [ 1.1900E-02 4.9076E-04 2.0081E-02 1.0365E-03 ].

Inertia, friction factor, pole pairs

Inertia coefficient J (kg.m²), friction factor F (N.m.s), and the number of pole pairs p. The friction torque Tf is proportional to the rotor speed ω (Tf = F.ω.) Tf is expressed in N.m, F in N.m.s, and ω in rad/s). Default is [ 3.895e6 0 20 ].

Initial conditions

Initial speed deviation Δω (% of nominal speed), electrical angle of the rotor Θe (degrees), line current magnitudes ia, ib, ic (A) and phase angles pha, phb, phc (degrees), and the initial field voltage Vf (V). You can compute these values automatically by using the Load Flow tool or the Machine Initialization tool of the powergui block. Default is [ 0 0 0 0 0 0 0 0 70.3192 ] .

You can specify the initial field voltage in one of two ways. If you know the nominal field current (first line, last parameter), in the dialog box, enter the initial field voltage in volts DC referred to the rotor. Otherwise, enter a zero as the nominal field current, and specify the initial field voltage in volts DC referred to the stator. You can determine the nominal field voltage viewed from the stator by selecting the Display Vfd which produces a nominal Vt check box on the Advanced tab.

Simulate saturation

Specifies whether magnetic saturation of the rotor and stator iron is to be simulated or not. Default is cleared.

[ifd; Vt]

No-load saturation curve parameters. Magnetic saturation of the stator and rotor iron is modeled by a piecewise linear relationship specifying points on the no-load saturation curve. The first row of this matrix contains the values of field currents. The second row contains values of corresponding terminal voltages. The first point (first column of the matrix) must be different from [0,0]. This point corresponds to the point where the effect of saturation begins. Default is [695.64,774.7,917.5,1001.6,1082.2,1175.9,1293.6,1430.2,1583.7;9660,10623,12243,13063,13757,14437,15180,15890,16567].

You must select the Simulate saturation check box to simulate saturation. Selecting this check box allows you to enter the matrix of parameters for simulating the saturation. If you do not want to model saturation in your simulation, do not select the Simulate saturation check box. In this case, the relationship between the ifd and Vt obtained is linear (no saturation).

Click Plot to view the no-load saturation curve.

Parameters for Synchronous Machine pu Fundamental

Nominal power, line-to-line voltage, and frequency

Total three-phase apparent power (VA), RMS line-to-line voltage (V), frequency (Hz), and field current (A).

This line is identical to the first line of the fundamental parameters in SI dialog box, except that you do not specify a nominal field current. This value is not required here because we do not need the transformation ratio. Since rotor quantities are viewed from the stator, they are converted to pu using the stator base quantities derived from the preceding three nominal parameters. Default is [ 187E6 13800 60].

Stator

Resistance Rs (Ω), leakage inductance Lls (H), and d-axis and q-axis magnetizing inductances Lmd (H) and Lmq (H), and Canay inductance. If the value of the Canay inductance in not known, you must enter 0 or leave it blank. Default is [ 2.85E-03 0.114 1.19 0.36 ].

Field

Field resistance Rf (Ω) and leakage inductance Llfd (H), both referred to the stator. Default is [ 5.79E-04 0.114].

Dampers

The d-axis resistance Rkd (Ω) and leakage inductance Llkd (H), the q-axis resistance Rkq1 (Ω) and leakage inductance Llkq1 (H), and (only if round rotor) the q-axis resistance Rkq2 (Ω) and leakage inductance Llkq2 (H). All of these values are referred to the stator. Default is [ 1.17E-02 0.182 1.97E-02 0.384 ].

Inertia coefficient, friction factor, pole pairs

Inertia constant H (s), which is the ratio of energy stored in the rotor at nominal speed over the nominal power of the machine, friction factor F (pu torque/pu speed), and the number of pole pairs p. Friction torque Tf is proportional to rotor speed ω (Tf=F.ω, where all quantities are expressed in pu). Default is [ 3.7 0 20].

Initial conditions

Initial speed deviation Δω (% of nominal speed), electrical angle of the rotor Θe (degrees), line current magnitudes ia, ib, ic (pu) and phase angles pha, phb, phc (degrees), and the initial field voltage Vf (pu). You can compute these values automatically by using the Load Flow tool or the Machine Initialization tool of the powergui block. Default is [ 0 0 0 0 0 0 0 0 1 ].

You can specify the initial field voltage in one of two ways. If you know the nominal field current (first line, last parameter), in the dialog box, enter the initial field voltage in volts DC referred to the rotor. Otherwise, enter a zero as the nominal field current, and specify the initial field voltage in volts DC referred to the stator. You can determine the nominal field voltage viewed from the stator by selecting the Display Vfd which produces a nominal Vt check box on the Advanced tab. For saturation, the nominal field current and nominal RMS line-to-line voltage are the base values for the field current and terminal voltage, respectively.

Simulate saturation

Specifies whether magnetic saturation of the rotor and stator iron is to be simulated or not. Default is cleared.

[ifd; Vt]

No-load saturation curve parameters. Magnetic saturation of the stator and rotor iron is modeled by a piecewise linear relationship specifying points on the no-load saturation curve. The first row of this matrix contains the values of field currents (in pu). The second row contains values of corresponding terminal voltages (in pu). The first point (first column of the matrix) must be different from [0,0]. This point corresponds to the point where the effect of saturation begins. Default is [0.6404,0.7127,0.8441,0.9214,0.9956,1.082,1.19,1.316,1.457;0.7,0.7698,0.8872,0.9466,0.9969,1.046,1.1,1.151,1.201].

You must select the Simulate saturation check box to simulate saturation. Selecting this check box allows you to enter the matrix of parameters for simulating the saturation. If you do not want to model saturation in your simulation, do not select the Simulate saturation check box. In this case, the relationship between the ifd and Vt obtained is linear (no saturation). For saturation, the nominal field current and nominal RMS line-to-line voltage are the base values for the field current and terminal voltage, respectively.

Click Plot to view the no-load saturation curve.

Parameters for Synchronous Machine pu Standard

Nominal power, line-to-line voltage, and frequency

Total three-phase apparent power (VA), RMS line-to-line voltage (pu), frequency (Hz), and field current (pu).

This line is identical to the first line of the fundamental parameters in SI dialog box, except that you do not specify a nominal field current. This value is not required here because we do not need the transformation ratio. Since rotor quantities are viewed from the stator, they are converted to pu using the stator base quantities derived from the preceding three nominal parameters. Default is [6e+04 400 50].

Reactances

The d-axis synchronous reactance Xd, transient reactance Xd', and subtransient reactance Xd'', the q-axis synchronous reactance Xq, transient reactance Xq' (only if round rotor), and subtransient reactance Xq'', and finally the leakage reactance Xl (all in pu). Default is [2.24 0.17 0.12 1.02 0.13 0.08].

d-axis time constants; q-axis time constant(s)

Specify the time constants you supply for each axis: either open-circuit or short-circuit. Choices are Short-circuit (default) or Open-circuit.

[ Td' Td'' Tq'' ] (s)

The d-axis and q-axis time constants (all in s). These values must be consistent with choices made on the two previous lines: d-axis transient open-circuit (Tdo') or short-circuit (Td') time constant, d-axis subtransient open-circuit (Tdo'') or short-circuit (Td'') time constant, q-axis transient open-circuit (Tqo') or short-circuit (Tq') time constant (only if round rotor), q-axis subtransient open-circuit (Tqo'') or short-circuit (Tq'') time constant. Default is [0.012 0.003 0.003].

Stator resistance

Stator resistance Rs (pu). Default is 0.037875.

Inertia coefficient, friction factor, pole pairs

Inertia constant H (s), which is the ratio of energy stored in the rotor at nominal speed over the nominal power of the machine, friction factor F (pu torque/pu speed), and the number of pole pairs p. Friction torque Tf is proportional to rotor speed ω (Tf=F.ω, where all quantities are expressed in pu). Default is [0.1028 0.02056 2].

Initial conditions

Initial speed deviation Δω (% of nominal speed), electrical angle of the rotor Θe (degrees), line current magnitudes ia, ib, ic (pu) and phase angles pha, phb, phc (degrees), and the initial field voltage Vf (pu). You can compute these values automatically by using the Load Flow tool or the Machine Initialization tool of the powergui block. Default is [ 0 0 0 0 0 0 0 0 1 ] .

You can specify the initial field voltage in one of two ways. If you know the nominal field current (first line, last parameter), in the dialog box, enter the initial field voltage in volts DC referred to the rotor. Otherwise, enter a zero as the nominal field current, and specify the initial field voltage in volts DC referred to the stator. You can determine the nominal field voltage viewed from the stator by selecting the Display Vfd which produces a nominal Vt check box on the Advanced tab. For saturation, the nominal field current and nominal RMS line-to-line voltage are the base values for the field current and terminal voltage, respectively.

Simulate saturation

Specifies whether magnetic saturation of the rotor and stator iron is to be simulated or not. Default is selected.

[ifd; Vt]

No-load saturation curve parameters. Magnetic saturation of the stator and rotor iron is modeled by a piecewise linear relationship specifying points on the no-load saturation curve. The first row of this matrix contains the values of field currents (in pu). The second row contains values of corresponding terminal voltages (in pu). The first point (first column of the matrix) must be different from [0,0]. This point corresponds to the point where the effect of saturation begins. Default is [0.6404,0.7127,0.8441,0.9214,0.9956,1.082,1.19,1.316,1.457;0.7,0.7698,0.8872,0.9466,0.9969,1.046,1.1,1.151,1.201].

You must select the Simulate saturation check box to simulate saturation. Selecting this check box allows you to enter the matrix of parameters for simulating the saturation. If you do not want to model saturation in your simulation, do not select the Simulate saturation check box. In this case, the relationship between the ifd and Vt obtained is linear (no saturation). For saturation, the nominal field current and nominal RMS line-to-line voltage are the base values for the field current and terminal voltage, respectively.

Click Plot to view the no-load saturation curve.

Advanced

The Advanced tab of the block is not visible when you set the Simulation type parameter of the powergui block to Continuous, or when you select the Automatically handle discrete solver parameter of the powergui block. The tab is visible when you set the Simulation type parameter of the powergui block to Discrete and when the Automatically handle discrete solver parameter of the powergui block is cleared.

Display nominal field current and voltage producing 1 pu stator voltage

Select to determine the nominal field current and voltage viewed from the stator. This parameter is visible only for the Synchronous Machine SI Fundamental block. Default is cleared.

As an example, without saturation, a typical curve might display as in the following figure. ifn is 1087 A and Vn is 13800 V RMS line-to-line, which is also 11268 V peak line-to-neutral.

Saturation is modeled as a piecewise linear saturation curve by using two lookup tables implementing variations of Lmd and Lmq magnetizing inductances.

The next figure illustrates the good fit graphically (the diamonds are the actual points entered in the dialog box).

In this particular case, the following values are used:

ifn	1087 A
ifd	[695.64, 774.7, 917.5, 1001.6, 1082.2, 1175.9, 1293.6, 1430.2, 1583.7] A
Vt	[9660, 10623, 12243, 13063, 13757, 14437, 15180, 15890, 16567] V

Sample time (−1 for inherited)

Specifies the sample time used by the block. To inherit the sample time specified in the powergui block, set this parameter to −1 (default).

Discrete solver model

Specifies the integration method used by the block when the Solver type parameter of the powergui block is set to Discrete. The choices are Trapezoidal non iterative (default), Trapezoidal iterative (alg. loop), Trapezoidal robust, and Backward Euler robust.

The Discrete solver model is automatically set to Trapezoidal robust when you select the Automatically handle Discrete solver parameter of the powergui block.

The Trapezoidal non iterative and Trapezoidal iterative (alg. loop) methods are no longer recommended for discretizing the Asynchronous Machine block. The first method requires you to add non-negligible shunt loads at the machine terminals to guarantee simulation stability, and the second method may fail to converge (simulation stops) when the number of machines increases in the model.

The Trapezoidal robust and Backward Euler robust methods allow you to eliminate the need to use parasitic loads and allow simulating a machine without loads. To eliminate topological errors of machines connected to an inductive circuit (for example, a circuit breaker connected in series with the machine); the machine models a negligible internal load of 0.01% of nominal power.

The Trapezoidal robust method is slightly more accurate than the Backward Euler robust method, especially when the model is simulated at larger sample times. The Trapezoidal robust method may produce slight damped numerical oscillations on machine voltage at no-load conditions, while the Backward Euler robust method prevents oscillations and maintains good accuracy.

For more information on what method to use in your application, see Simulating Discretized Electrical Systems.

Load Flow

The load flow parameters are used to define block parameters for use with the Load Flow tool of the powergui block. These load flow parameters are used for model initialization only. They have no impact on the block model and on the simulation performance.

The configuration of the Load Flow tab depends on the option selected for the Generator type parameter.

Generator type

Specify the generator type of the machine.

Select swing to implement a generator controlling magnitude and phase angle of its terminal voltage. The reference voltage magnitude and angle are specified by the Swing bus or PV bus voltage and Swing bus voltage angle parameters of the Load Flow Bus block connected to the machine terminals.

Select PV (default) to implement a generator controlling its output active power P and voltage magnitude V. P is specified by the Active power generation P parameter of the block. V is specified by the Swing bus or PV bus voltage parameter of the Load Flow Bus block connected to the machine terminals. You can control the minimum and maximum reactive power generated by the block by using the Minimum reactive power Qmin and Maximum reactive power Qmax parameters.

Select PQ to implement a generator controlling its output active power P and reactive power Q. P and Q are specified by the Active power generation P and Reactive power generation Q parameters of the block, respectively.

Active power generation P

Specify the active power that you want generated by the machine, in watts. When the machine operates in motor mode, you specify a negative value. This parameter is available if you specify Generator type as PV or PQ. Default is 0.

Reactive power generation Q

Specify the reactive power that you want generated by the machine, in vars. A negative value indicates that the reactive power is absorbed by the machine. This parameter is available only if you specify Generator type as PQ. Default is 0.

Minimum reactive power Qmin

This parameter is available only if you specify Generator type as PV. Indicates the minimum reactive power that can be generated by the machine while keeping the terminal voltage at its reference value. This reference voltage is specified by the Swing bus or PV bus voltage parameter of the Load Flow Bus block connected to the machine terminals. The default value is -inf, which means that there is no lower limit on the reactive power output. Default is -inf.

Maximum reactive power Qmax

This parameter is available only if you specify Generator type as PV. Indicates the maximum reactive power that can be generated by the machine while keeping the terminal voltage at its reference value. This reference voltage is specified by the Swing bus or PV bus voltage parameter of the Load Flow Bus block connected to the machine terminals. The default value is inf, which means that there is no upper limit on the reactive power output. Default is inf.

Inputs and Outputs

The units of inputs and outputs vary according to which dialog box you use to enter the block parameters. If you choose to specify fundamental parameters in SI units, the relevant inputs and outputs are in SI units. The dw in the vector of internal variables is in pu, and angle Θ is in rad. The other inputs and outputs are in pu.

Pm

The first Simulink input is the mechanical power at the machine's shaft, in W or pu. In generating mode, this input can be a positive constant or function or the output of a prime mover block (see the Hydraulic Turbine and Governor or Steam Turbine and Governor blocks). In motoring mode, this input is usually a negative constant or function.

w

The alternative block input instead of Pm (depending on the value of the Mechanical input parameter) is the machine speed, in rad/s.

Vf

The second Simulink input of the block is the field voltage. This voltage can be supplied by a voltage regulator in generator mode (see the Excitation System block). It is usually a constant in motor mode.

If you use the model in SI fundamental units, the field voltage Vf must be entered in volts DC if nominal field current Ifn is specified, or in volts referred to stator if Ifn is not specified. To obtain the Vfd producing nominal voltage, select the Display nominal field current and voltage producing 1 pu stator voltage check box in the Advanced tab. If you use the model in pu Standard or in pu Fundamental units, Vf must be entered in pu (1 pu of field voltage producing 1 pu of terminal voltage at no load).

m

The Simulink output of the block is a vector containing measurement signals. You can demultiplex these signals by using the Bus Selector block provided in the Simulink library. Depending on the type of mask that you use, the units are in SI or in pu.

Name	Definition	Units
ias	Stator current is_a	A or pu
ibs	Stator current is_b	A or pu
ics	Stator current is_c	A or pu
iq	Stator current iq	A or pu
id	Stator current id	A or pu
ifd	Field current ifd	A or pu
ikq1	Damper winding current ikq1	A or pu
Ikq2	Damper winding current ikq2	A or pu
ikd	Damper winding current ikd	A or pu
phimq	Mutual flux phimq	V.s or pu
phimd	Mutual flux phimd	V.s or pu
vq	Stator voltage vq	V or pu
vd	Stator voltage vd	V or pu
lmq	Lmq saturated inductance	H or pu
lmd	Lmd saturated inductance	H or pu
dtheta	Rotor angle deviation d_theta	rad
w	Rotor speed wm	rad/s or pu
Pe	Electrical power Pe	W or pu
dw	Rotor speed deviation dw	pu
theta	Rotor mechanical angle theta	degree
Te	Electromagnetic torque Te	N.m or pu
delta	Load angle delta	degree
Pe0	Output active power Peo	W or pu
Qe0	Output reactive power Qeo	VAR or pu

The angular deviation of the rotor angle theta represents the electrical angle giving the rotor's instantaneous position with respect to a common reference rotating at synchronous speed. This angle is useful in stability studies to measure the relative positions of the rotors of different machines in a network. The positions of the rotors are then measured with respect to the theta position of a given machine chosen as a reference.

Limitations

In Discrete systems, when you use Synchronous Machine blocks discretized with the trapezoidal non-iterative solver, you might have to use a small parasitic resistive load, connected at the machine terminals, to avoid numerical oscillations. Large sample times require larger loads. The minimum resistive load is proportional to the sample time. As a rule of thumb, remember that with a 25 μs time step on a 60-Hz system, the minimum load is approximately 2.5 percent of the machine nominal power. For example, a 200 MVA synchronous machine in a power system discretized with a 50 μs sample time requires approximately 5 percent of resistive load or 10 MW. If the sample time is reduced to 20 μs, a resistive load of 4 MW should be sufficient.

However, if you discretize the Synchronous Machine block using the trapezoidal iterative (alg. loop) solver, you can use a negligible parasitic load (below 0.1% of nominal power) while preserving numerical stability. This iterative model producing an algebraic loop results in slower simulation speed.

Example 1

The power_SM_Fundamental example shows the use of the Synchronous Machine SI Fundamental block and the Synchronous Machine pu Fundamental block to model a 555 MVA, 24 kV, 60 Hz, 3600-rpm synchronous generator. It shows how to specify SI and pu parameters. It also explains how to compute field and damper rotor winding parameters that are referred to the stator. In addition to the field winding, the round rotor of this machine has three damper windings: one damper in the direct axis and two dampers in the quadrature axis.

Three circuits simulate the same synchronous machine:

Circuit 1: Fundamental parameters are specified in SI. The nominal field current is specified (ifn = 1300 A).
Circuit 2: Fundamental parameters are specified in SI. The nominal field current is not specified (ifn = 0).
Circuit 3: Fundamental parameters are specified in pu.

Machine parameters are taken from an example in Kundur [5].

Look at the Model Properties/PreLoad Fcn callback section of the model to see machine specifications and the computation of stator and field bases, RL rotor parameters referred to the stator, transformation ratio, and nominal field voltage and current.

The machines initially operate in steady state at virtually no load (load = 0. 1% of nominal power) with constant field voltage and mechanical power. A phase-to-phase 6-cycle fault is applied at t = 0.1 sec. The Scope shows the comparison between line-to-line AB voltage, phase A stator current, and field current of the three machines.

To simulate the discrete model, select Discrete simulation type in the powergui block. The model is discretized with a sample time Ts = 50 μs. To obtain a stable model with such a small load (0. 1% of nominal power), select the Trapezoidal iterative (alg. Loop) discrete solver in the Advanced tab of each Synchronous Machine block.

Example 2

The power_syncmachine example illustrates the use of the Synchronous Machine block in motor mode. The simulated system consists of an industrial grade synchronous motor (150 HP (112 kVA), 762 V) connected to a network with a 10 MVA short-circuit level. The machine is initialized for an output electrical power of −50 kW (negative value for motor mode), corresponding to a mechanical power of −48.9 kW. The corresponding values of mechanical power and field voltage are specified by the Pm Step block and in the Vf Constant block. The Pm Step block applies a sudden increase of mechanical power from −48.9 kW to −60 kW at time t = 0.1 s.

Run the simulation.

After the load has increased from 48.9 kW to 60 kW at t = 0.1 s, the machine speed oscillates before stabilizing to 1800 rpm. The load angle (angle between terminal voltage and internal voltage) increases from −21 degrees to −53 degrees.

References

[1] I.M. Canay. "Causes of Discrepancies on Calculation of Rotor Quantities and Exact Equivalent Diagrams of the Synchronous Machine." IEEE^®Transactions on Power Apparatus and Systems. PAS-88, no. 7 (1969): 1114–1120.

[2] Moeini, A., et al. “Synchronous Machine Stability model, an Update to IEEE Std 1110-2002 Data Translation Technique.” IEEE standards panel sessions. 2018 IEEE PES.

[3] IEEE Guide for Synchronous Generator Modeling Practices and Applications in Power System Stability Analyses. IEEE Std 1110-2002 (Revision of IEEE Std 1110-1991 [2003]): 1–72.

[4] Krause, P.C. Analysis of Electric Machinery. Section 12.5. New York: McGraw-Hill, 1986.

[5] Kundur, P. Power System Stability and Control. New York, McGraw-Hill, 1994.

Documentation

Synchronous Machine

Library

Description

Dynamic Model with Unequal Mutual Inductance

Base Values, Transformation Ratio, and Rotor Parameters Referred to the Stator

Stator Base Values

Stator/Field Transformation Ratio

Field Base Values

Field Voltage, Current, and RL Values Referred to the Stator

Field Voltage and Current for SI Fundamental Synchronous Machine

Field Voltage and Current for PU Fundamental Synchronous Machine

Parameters

Configuration

Parameters for Synchronous Machine SI Fundamental

Parameters for Synchronous Machine pu Fundamental

Parameters for Synchronous Machine pu Standard

Advanced

Load Flow

Inputs and Outputs

Limitations

Example 1

Example 2

References

See Also

Simscape Electrical Documentation

Support