cordicrotate

Rotate input using CORDIC-based approximation

collapse all in page

Syntax

v = cordicrotate(theta,u)
v = cordicrotate(theta,u,niters)
v = cordicrotate(theta,u,Name,Value)
v = cordicrotate(theta,u,niters,Name,Value)

Description

v = cordicrotate(theta,u) rotates the input u by theta using a CORDIC algorithm approximation. The function returns the result of u .* e^(j*theta).

v = cordicrotate(theta,u,niters) performs niters iterations of the algorithm.

v = cordicrotate(theta,u,Name,Value) scales the output depending on the Boolean value, b.

v = cordicrotate(theta,u,niters,Name,Value) specifies both the number of iterations and the Name,Value pair for whether to scale the output.

Input Arguments

theta

theta can be a signed or unsigned scalar, vector, matrix, or N-dimensional array containing the angle values in radians. All values of theta must be in the range [–2π 2π).

u

u can be a signed or unsigned scalar value or have the same dimensions as theta. u can be real or complex valued.

niters

niters is the number of iterations the CORDIC algorithm performs. This argument is optional. When specified, niters must be a positive, integer-valued scalar. If you do not specify niters, or if you specify a value that is too large, the algorithm uses a maximum value. For fixed-point operation, the maximum number of iterations is the word length of u or one less than the word length of theta, whichever is smaller. For floating-point operation, the maximum value is 52 for double or 23 for single. Increasing the number of iterations can produce more accurate results, but it also increases the expense of the computation and adds latency.

Name-Value Pair Arguments

Optional comma-separated pairs of Name,Value arguments, where Name is the argument name and Value is the corresponding value. Name must appear inside single quotes ('').

'ScaleOutput'

ScaleOutput is a Boolean value that specifies whether to scale the output by the inverse CORDIC gain factor. This argument is optional. If you set ScaleOutput to true or 1, the output values are multiplied by a constant, which incurs extra computations. If you set ScaleOutput to false or 0, the output is not scaled.

Default: true

Output Arguments

v

v contains the approximated result of the CORDIC rotation algorithm. When the input u is floating point, the output v has the same data type as the input.

When the input u is a signed integer or fixed point data type, the output v is a signed fi object. This fi object has a word length that is two bits larger than that of u. Its fraction length is the same as the fraction length of u.

When the input u is an unsigned integer or fixed point, the output v is a signed fi object. This fi object has a word length that is three bits larger than that of u. Its fraction length is the same as the fraction length of u.

Examples

Run the following code, and evaluate the accuracy of the CORDIC-based complex rotation.

wrdLn = 16;
theta = fi(-pi/3, 1, wrdLn);
u     = fi(0.25 - 7.1i, 1, wrdLn);
uTeTh = double(u) .* exp(1i * double(theta));

fprintf('\n\nNITERS\tReal\t ERROR\t LSBs\t\tImag\tERROR\tLSBs\n');
fprintf('------\t-------\t ------\t ----\t\t-------\t------\t----\n');
for niters = 1:(wrdLn - 1)
 v_fi   = cordicrotate(theta, u, niters);
 v_dbl  = double(v_fi);
 x_err  = abs(real(v_dbl) - real(uTeTh));
  y_err  = abs(imag(v_dbl) - imag(uTeTh));
 fprintf('%d\t%1.4f\t %1.4f\t %1.1f\t\t%1.4f\t %1.4f\t %1.1f\n',...
   niters, real(v_dbl),x_err,(x_err * pow2(v_fi.FractionLength)), ...
   imag(v_dbl),y_err, (y_err * pow2(v_fi.FractionLength)));
end
fprintf('\n');

The output table appears as follows:

NITERS  Real     ERROR    LSBs    Imag     ERROR    LSBs
------	-------	 ------	 ----		-------	 ------	 ------
1      -4.8438   1.1800   4833.5  -5.1973  1.4306  5859.8
2      -6.6567   0.6329   2592.5  -2.4824  1.2842  5260.2
3      -5.8560   0.1678   687.5   -4.0227  0.2560  1048.8
4      -6.3098   0.2860   1171.5  -3.2649  0.5018  2055.2
5      -6.0935   0.0697   285.5   -3.6528  0.1138  466.2
6      -5.9766   0.0472   193.5   -3.8413  0.0746  305.8
7      -6.0359   0.0121   49.5    -3.7476  0.0191  78.2
8      -6.0061   0.0177   72.5    -3.7947  0.0280  114.8
9      -6.0210   0.0028   11.5    -3.7710  0.0043  17.8
10     -6.0286   0.0048   19.5    -3.7590  0.0076  31.2
11     -6.0247   0.0009   3.5   	 -3.7651  0.0015  6.2
12     -6.0227   0.0011   4.5  	  -3.7683  0.0017  6.8
13     -6.0237   0.0001   0.5   	 -3.7666  0.0001  0.2
14     -6.0242   0.0004   1.5   	 -3.7656  0.0010  4.2
15     -6.0239   0.0001   0.5   	 -3.7661  0.0005  2.2

More About

collapse all

CORDIC

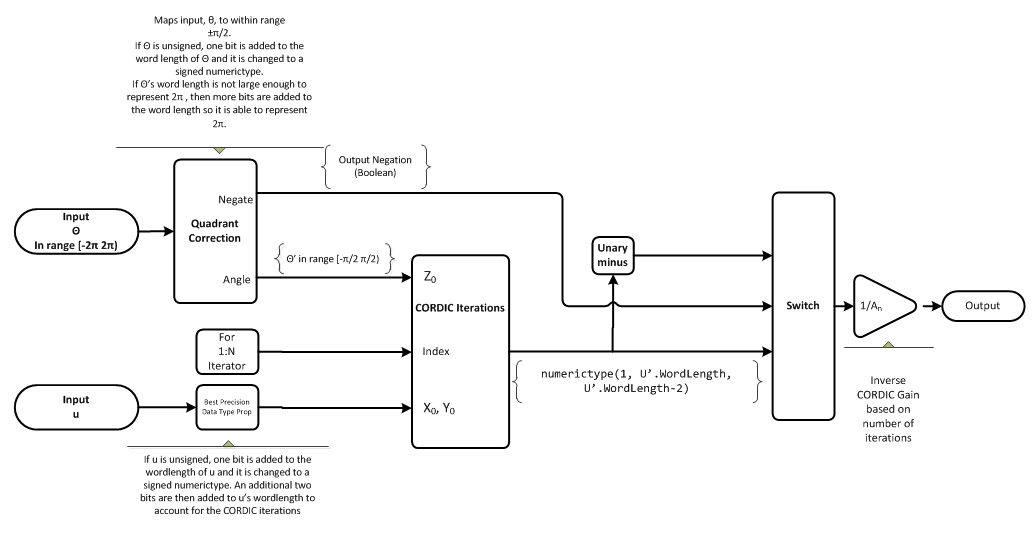
CORDIC is an acronym for COordinate Rotation DIgital Computer. The Givens rotation-based CORDIC algorithm is one of the most hardware-efficient algorithms available because it requires only iterative shift-add operations (see References). The CORDIC algorithm eliminates the need for explicit multipliers. Using CORDIC, you can calculate various functions, such as sine, cosine, arc sine, arc cosine, arc tangent, and vector magnitude. You can also use this algorithm for divide, square root, hyperbolic, and logarithmic functions.

Increasing the number of CORDIC iterations can produce more accurate results, but doing so also increases the expense of the computation and adds latency.

Algorithms

collapse all

Signal Flow Diagrams

CORDIC Rotation Kernel

X represents the real part, Y represents the imaginary part, and Z represents theta. This algorithm takes its initial values for X, Y, and Z from the inputs, u and theta.

fimath Propagation Rules

CORDIC functions discard any local fimath attached to the input.

The CORDIC functions use their own internal fimath when performing calculations:

  • OverflowAction—Wrap

  • RoundingMethod—Floor

The output has no attached fimath.

References

[1] Volder, JE. “The CORDIC Trigonometric Computing Technique.” IRE Transactions on Electronic Computers. Vol. EC-8, September 1959, pp. 330–334.

[2] Andraka, R. “A survey of CORDIC algorithm for FPGA based computers.” Proceedings of the 1998 ACM/SIGDA sixth international symposium on Field programmable gate arrays. Feb. 22–24, 1998, pp. 191–200.

[3] Walther, J.S. “A Unified Algorithm for Elementary Functions.” Hewlett-Packard Company, Palo Alto. Spring Joint Computer Conference, 1971, pp. 379–386. (from the collection of the Computer History Museum). www.computer.org/csdl/proceedings/afips/1971/5077/00/50770379.pdf

[4] Schelin, Charles W. “Calculator Function Approximation.” The American Mathematical Monthly. Vol. 90, No. 5, May 1983, pp. 317–325.

Extended Capabilities

See Also

|

Introduced in R2011a

Fixed-Point Designer Documentation

Support