Multirate Filters
Why Are Multirate Filters Needed?
Multirate filters can bring efficiency to a particular filter implementation. In general, multirate filters are filters in which different parts of the filter operate at different rates. The most obvious application of such a filter is when the input sample rate and output sample rate need to differ (decimation or interpolation) — however, multirate filters are also often used in designs where this is not the case. For example you may have a system where the input sample rate and output sample rate are the same, but internally there is decimation and interpolation occurring in a series of filters, such that the final output of the system has the same sample rate as the input. Such a design may exhibit lower cost than could be achieved with a single-rate filter for various reasons. For more information about the relative cost benefit of using multirate filters, see Harris, Fredric J., Multirate Signal Processing for Communication Systems, Prentice Hall PTR, 2004.
Overview of Multirate Filters
A filter that reduces the input rate is called a decimator. A filter that increases the input rate is called an interpolator. To visualize this process, examine the following figure, which illustrates the processes of interpolation and decimation in the time domain.
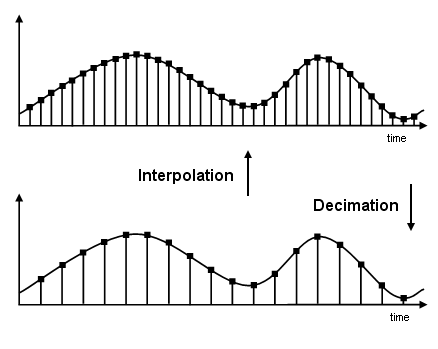
If you start with the top signal, sampled at a frequency
Fs, then the bottom signal is sampled at
Fs/2 frequency. In this case, the decimation factor, or
M, is 2.
The following figure illustrates effect of decimation in the frequency domain.
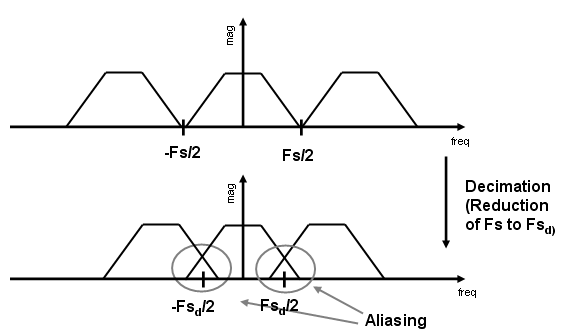
In the first graphic in the figure you can see a signal that is critically sampled, i.e. the sample rate is equal to two times the highest frequency component of the sampled signal. As such the period of the signal in the frequency domain is no greater than the bandwidth of the sampling frequency. When reduce the sampling frequency (decimation), aliasing can occur, where the magnitudes at the frequencies near the edges of the original period become indistinguishable, and the information about these values becomes lost. To work around this problem, the signal can be filtered before the decimation process, avoiding overlap of the signal spectra at Fs/2.
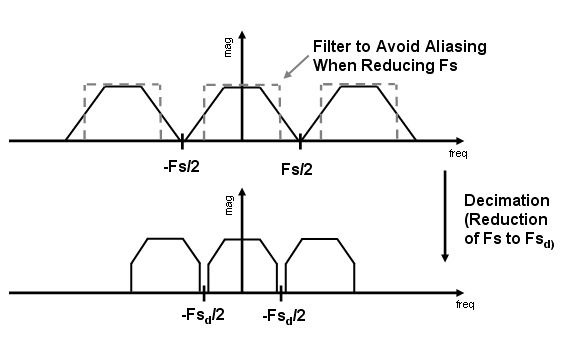
An analogous approach must be taken to avoid imaging when performing interpolation on a sampled signal. For more information about the effects of decimation and interpolation on a sampled signal, see References.
The following list summarizes some guidelines and general requirements regarding decimation and interpolation:
By the Nyquist Theorem, for band-limited signals, the sampling frequency must be at least twice the bandwidth of the signal. For example, if you have a lowpass filter with the highest frequency of 10 MHz, and a sampling frequency of 60 MHz, the highest frequency that can be handled by the system without aliasing is 60/2=30, which is greater than 10. You could safely set M=2 in this case, since (60/2)/2=15, which is still greater than 10.
If you wish to decimate a signal which does not meet the frequency criteria, you can either:
Interpolate first, and then decimate
When decimating, you should apply the filter first, then perform the decimation. When interpolating a signal, you should interpolate first, then filter the signal.
Typically in decimation of a signal a filter is applied first, thereby allowing decimation without aliasing, as shown in the following figure:

Conversely, a filter is typically applied after interpolation to avoid imaging:
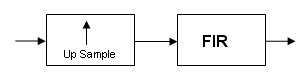
M must be an integer. Although, if you wish to obtain an M of 4/5, you could interpolate by 4, and then decimate by 5, provided that frequency restrictions are met. This type of multirate filter will be referred to as a sample rate converter in the documentation that follows.
Multirate filters are most often used in stages. This technique is introduced in the following section.
References
[1] Fliege, N.J., Multirate Digital Signal Processing, John Wiley and Sons, 1994.
[2] Harris, Fredric J, Multirate Signal Processing for Communication Systems, Prentice Hall PTR, 2004.
[3] Hogenauer, E. B., “An Economical Class of Digital Filters for Decimation and Interpolation,” IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. ASSP-29, No. 2, April 1981, pp. 155-162.
[4] Lyons, Richard G., Understanding Digital Signal Processing, Prentice Hall PTR, 2004
[5] Mitra, S.K., Digital Signal Processing, McGraw-Hill, 1998.
[6] Orfanidis, S.J., Introduction to Signal Processing, Prentice-Hall, Inc., 1996.