FFT

Fast Fourier transform (FFT) of input

Library:
DSP System Toolbox / Transforms

Description

The FFT block computes the fast Fourier transform (FFT) across the first dimension of an N-D input array, u. The block uses one of two possible FFT implementations. You can select an implementation based on the FFTW library or an implementation based on a collection of Radix-2 algorithms. To allow the block to choose the implementation, you can select Auto. For more information about the FFT implementations, see Algorithms.

For user-specified FFT lengths not equal to P, zero padding or truncating, or modulo-length data wrapping occurs before the FFT operation. For an FFT with P ≤ M:

y = fft(u,M) % P ≤ M

Wrapping:

y(:,L) = fft(datawrap(u(:,L),M)) % P > M; L = 1,...,N

Truncating:

y (:,L) = fft(u,M) % P > M; L = 1,...,N

Tip

When the input length, P, is greater than the FFT length, M, you may see magnitude increases in your FFT output. These magnitude increases occur because the FFT block uses modulo-M data wrapping to preserve all available input samples.

To avoid such magnitude increases, you can truncate the length of your input sample, P, to the FFT length, M. To do so, place a Pad block before the FFT block in your model.

Ports

Input

expand all

`Port_1` — Input signal
vector | matrix | N-D array

Input signal for computing the FFT. The block computes the FFT along the first dimension of the N-D input signal.

For more information on how the block computes the FFT, see Description and Algorithms.

Output

expand all

`Port_1` — FFT of input
vector | matrix | N-D array

The FFT, computed across the first dimension of an N-D input array. When the output of the block has an integer or fixed-point data type, it is always signed.

The kth entry of the Lth output channel, y(k,L), equals the kth point of the M-point discrete Fourier transform (DFT) of the Lth input channel:

$y (k, L) = \sum_{p = 1}^{P} u (p, L) e^{- j 2 π (p - 1) (k - 1) / M} k = 1, \dots, M$

For more information on how the block computes the FFT, see Description and Algorithms.

Data Types: single | double | int8 | int16 | int32 | fixed point
Complex Number Support: Yes

Parameters

expand all

Main

`FFT implementation` — FFT implementation
`Auto` (default) | `Radix-2` | `FFTW`

Set this parameter to FFTW to support an arbitrary length input signal. The block restricts generated code with FFTW implementation to host computers capable of running MATLAB^®.

Set this parameter to Radix-2 for bit-reversed processing, fixed or floating-point data, or portable C-code generation using the Simulink^® Coder™. The dimension M of the M-by-N input matrix, must be a power of two. To work with other input sizes, use the Pad block to pad or truncate these dimensions to powers of two, or if possible choose the FFTW implementation. For more information about the algorithms used by the Radix-2 mode, see Radix-2 Implementation.

Set this parameter to Auto to let the block choose the FFT implementation. For floating-point inputs with non-power-of-two transform lengths, the FFTW algorithm is automatically chosen. Otherwise a Radix-2 algorithm is automatically chosen. For non-power-of-two transform lengths, the block restricts generated code to MATLAB host computers.

`Output in bit-reversed order` — Output in bit-reversed order
`off` (default) | `on`

Designate the order of the output channel elements relative to the ordering of the input elements. When you select this check box, the output channel elements appear in bit-reversed order relative to the input ordering. If you clear this check box, the output channel elements appear in linear order relative to the input ordering.

Note

The FFT block calculates its output in bit-reversed order. Linearly ordering the FFT block output requires an extra bit-reversal operation. In many situations, you can increase the speed of the FFT block by selecting the Output in bit-reversed order check box.

For more information ordering of the output, see Linear and Bit-Reversed Output Order.

Dependencies

To enable this parameter, set FFT implementation to Auto or Radix-2.

`Divide output by FFT length` — Divide output by FFT length
`off` (default) | `on`

When you select this parameter, the block divides the output of the FFT by the FFT length. This option is useful when you want the output of the FFT to stay in the same amplitude range as its input. This is particularly useful when working with fixed-point data types.

`Inherit FFT length from input dimensions` — Inherit FFT length from input dimensions
`on` (default) | `off`

Select to inherit the FFT length from the input dimensions. When you select this check box, the input length must be a power of two.

Dependencies

When you do not select this check box, the FFT length parameter becomes available to specify the length.

`FFT length` — FFT length
`64` (default) | integer

Specify FFT length as an integer greater than or equal to two.

When you set the FFT implementation parameter to Radix-2, or when you check the Output in bit-reversed order check box, this value must be a power of two.

Dependencies

To enable this parameter, clear the Inherit FFT length from input dimensions check box.

`Wrap input data when FFT length is shorter than input length` — Wrap or truncate input
`on` (default) | `off`

Choose to wrap or truncate the input, depending on the FFT length. If you select this parameter, modulo-length data wrapping occurs before the FFT operation when the FFT length is shorter than the input length. If you clear this check box, truncation of the input data to the FFT length occurs before the FFT operation.

Dependencies

To enable this parameter, clear the Inherit FFT length from input dimensions check box.

Data Types

`Rounding mode` — Rounding method
`Floor` (default) | `Ceiling` | `Convergent` | `Nearest` | `Round` | `Simplest` | `Zero`

Select the rounding mode for fixed-point operations.

Limitations

The sine table values do not obey this parameter; instead, they always round to Nearest.

The Rounding mode parameter has no effect on numeric results when all these conditions are met:

Product output data type is Inherit: Inherit via internal rule.
Accumulator data type is Inherit: Inherit via internal rule.

With these data type settings, the block operates in full-precision mode.

`Saturate on integer overflow` — Saturate on integer overflow
`off` (default) | `on`

When you select this parameter, the block saturates the result of its fixed-point operation. When you clear this parameter, the block wraps the result of its fixed-point operation. For details on saturate and wrap, see overflow mode for fixed-point operations.

Limitations

The Saturate on integer overflow parameter has no effect on numeric results when all these conditions are met:

Product output data type is Inherit: Inherit via internal rule.
Accumulator data type is Inherit: Inherit via internal rule.

With these data type settings, the block operates in full-precision mode.

`Sine table` — Data type of sine table values
`Inherit: Same word length as input` (default) | `fixdt(1,16)`

Choose how to specify the word length of the values of the sine table. The fraction length of the sine table values always equals the word length minus one. You can set this parameter to:

A rule that inherits a data type, for example, Inherit: Same word length as input
An expression that evaluates to a valid data type, for example, fixdt(1,16)

Click the Show data type assistant button to display the Data Type Assistant, which helps you set the Sine table parameter.

See Specify Data Types Using Data Type Assistant (Simulink) for more information.

Limitations

The sine table values do not obey the Rounding mode and Saturate on integer overflow parameters; instead, they are always saturated and rounded to Nearest.

`Product output` — Product output data type
`Inherit: Inherit via internal rule` (default) | `Inherit: Same as input` | `fixdt(1,16,0)`

Specify the product output data type. See Fixed Point and Multiplication Data Types for illustrations depicting the use of the product output data type in this block. You can set this parameter to:

A rule that inherits a data type, for example, Inherit: Inherit via internal rule. For more information on this rule, see Inherit via Internal Rule.
An expression that evaluates to a valid data type, for example, fixdt(1,16,0)

Click the Show data type assistant button to display the Data Type Assistant, which helps you set the Product output parameter.

See Specify Data Types Using Data Type Assistant (Simulink) for more information.

`Accumulator` — Accumulator data type
`Inherit: Inherit via internal rule` (default) | `Inherit: Same as input` | `Inherit: Same as product output` | `fixdt(1,16,0)`

Specify the accumulator data type. See Fixed Point for illustrations depicting the use of the accumulator data type in this block. You can set this parameter to:

A rule that inherits a data type, for example, Inherit: Inherit via internal rule. For more information on this rule, see Inherit via Internal Rule.
An expression that evaluates to a valid data type, for example, fixdt(1,16,0)

Click the Show data type assistant button to display the Data Type Assistant, which helps you set the Accumulator parameter.

See Specify Data Types Using Data Type Assistant (Simulink) for more information.

`Output` — Output data type
`Inherit: Inherit via internal rule` (default) | `Inherit: Same as input` | `fixdt(1,16,0)`

Specify the output data type. See Fixed Point for illustrations depicting the use of the output data type in this block. You can set this parameter to:

A rule that inherits a data type, for example, Inherit: Inherit via internal rule.
When you select Inherit: Inherit via internal rule, the block calculates the output word length and fraction length automatically. The equations that the block uses to calculate the ideal output word length and fraction length depend on the setting of the Divide output by FFT length check box.
- When you select the Divide output by FFT length check box, the ideal output word and fraction lengths are the same as the input word and fraction lengths.
- When you clear the Divide output by FFT length check box, the block computes the ideal output word and fraction lengths according to the following equations:
  $W L_{i d e a l o u t p u t} = W L_{i n p u t} + floor (\log_{2} (F F T l e n g t h - 1)) + 1$
  $F L_{i d e a l o u t p u t} = F L_{i n p u t}$
Using these ideal results, the internal rule then selects word lengths and fraction lengths that are appropriate for your hardware. For more information, see Inherit via Internal Rule.
An expression that evaluates to a valid data type, for example, fixdt(1,16,0)

Click the Show data type assistant button to display the Data Type Assistant, which helps you set the Output parameter.

See Control Signal Data Types (Simulink) for more information.

`Output Minimum` — Minimum value block should output
`[]` (default) | scalar

Specify the minimum value that the block should output. The default value is [] (unspecified). Simulink software uses this value to perform:

Simulation range checking (see Specify Signal Ranges (Simulink))
Automatic scaling of fixed-point data types

`Output Maximum` — Maximum value block should output
`[]` (default) | scalar

Specify the maximum value that the block should output. The default value is [] (unspecified). Simulink software uses this value to perform:

Simulation range checking (see Specify Signal Ranges (Simulink))
Automatic scaling of fixed-point data types

`Lock data type settings against changes by the fixed-point tools` — Prevent fixed-point tools from overriding data types
`off` (default) | `on`

Select this parameter to prevent the fixed-point tools from overriding the data types you specify on the block dialog.

Model Examples

Transform Time-Domain Data into Frequency Domain

Transform time-domain data into the frequency domain using the FFT block.

Block Characteristics

Data Types	`double` \| `fixed point` \| `integer` \| `single`
Direct Feedthrough	`no`
Multidimensional Signals	`yes`
Variable-Size Signals	`limited^[a]`
Zero-Crossing Detection	`no`
^[a] Variable-size signals are only supported when the Inherit FFT length from input dimensions checkbox is selected.

Algorithms

expand all

FFTW Implementation

The FFTW implementation provides an optimized FFT calculation including support for power-of-two and non-power-of-two transform lengths in both simulation and code generation. Generated code using the FFTW implementation can only run on computers capable of running MATLAB. The input data type must be floating-point.

Radix-2 Implementation

The Radix-2 implementation supports bit-reversed processing, fixed or floating-point data, and allows the block to provide portable C-code generation using the Simulink Coder. The dimension M of the M-by-N input matrix must be a power of two. To work with other input sizes, use the Pad block to pad or truncate these dimensions to powers of two, or if possible choose the FFTW implementation.

With Radix-2 selected, the block implements one or more of the following algorithms:

Butterfly operation
Double-signal algorithm
Half-length algorithm
Radix-2 decimation-in-time (DIT) algorithm
Radix-2 decimation-in-frequency (DIF) algorithm

Radix-2 Algorithms for Real and Complex Signals

Complexity of Input	Output Ordering	Algorithms Used for FFT Computation
Complex	Linear	Bit-reversed operation and radix-2 DIT
Complex	Bit-reversed	Radix-2 DIF
Real	Linear	Bit-reversed operation and radix-2 DIT in conjunction with the half-length and double-signal algorithms
Real	Bit-reversed	Radix-2 DIF in conjunction with the half-length and double-signal algorithms

The efficiency of the FFT algorithm can be enhanced for real input signals by forming complex-valued sequences from the real-valued sequences prior to the computation of the DFT. When there are 2N+1 real input channels, the FFT block forms these complex-valued sequences by applying the double-signal algorithm to the first 2N input channels, and the half-length algorithm to the last odd-numbered channel.

For real input signals with fixed-point data types, different numerical results might appear in the output of the last odd-numbered channel, even when all input channels are identical. This numerical difference results from differences in the double-signal algorithm and the half-length algorithm.

You can eliminate this numerical difference in two ways:

Using full precision arithmetic for fixed-point input signals
Changing the input data type to floating point

For more information on the double-signal algorithm, see [2], “Efficient Computation of the DFT of Two Real Sequences” on page 475. For more information on the half-length algorithm, see [2], “Efficient Computation of the DFT of a 2N-Point Real Sequence” on page 476.

Radix-2 Optimization for the Table of Trigonometric Values

In certain situations, the block’s Radix–2 algorithm computes all the possible trigonometric values of the twiddle factor

$e^{j \frac{2 π k}{K}}$

where K is the greater value of either M or N and $k = 0, \dots, K - 1$ . The block stores these values in a table and retrieves them during simulation. The number of table entries for fixed-point and floating-point is summarized in the following table:

Number of Table Entries for N-Point FFT
floating-point	3N/4
fixed-point	N

References

[1] Orfanidis, S. J. Introduction to Signal Processing. Upper Saddle River, NJ: Prentice Hall, 1996, p. 497.

[2] Proakis, John G. and Dimitris G. Manolakis. Digital Signal Processing, 3rd ed. Upper Saddle River, NJ: Prentice Hall, 1996.

[3] FFTW (http://www.fftw.org)

[4] Frigo, M. and S. G. Johnson, “FFTW: An Adaptive Software Architecture for the FFT,”Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Vol. 3, 1998, pp. 1381-1384.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Usage notes and limitations:

When the following conditions apply, the executable generated from this block relies on prebuilt dynamic library files (.dll files) included with MATLAB:
- FFT implementation is set to FFTW.
- Inherit FFT length from input dimensions is cleared, and FFT length is set to a value that is not a power of two.
Use the packNGo function to package the code generated from this block and all the relevant files in a compressed zip file. Using this zip file, you can relocate, unpack, and rebuild your project in another development environment where MATLAB is not installed. For more details, see How To Run a Generated Executable Outside MATLAB.
When the FFT length is a power of two, you can generate standalone C and C++ code from this block.

Fixed-Point Conversion
Design and simulate fixed-point systems using Fixed-Point Designer™.

The following diagrams show the data types used in the FFT block for fixed-point signals. You can set the Sine table, Accumulator, Product output, and Output data types displayed in the diagrams in the FFT dialog box as discussed in Parameters.

Inputs to the FFT block are first cast to the output data type and stored in the output buffer. Each butterfly stage then processes signals in the accumulator data type, with the final output of the butterfly being cast back into the output data type. The block multiplies in a twiddle factor before each butterfly stage in a decimation-in-time FFT and after each butterfly stage in a decimation-in-frequency FFT.

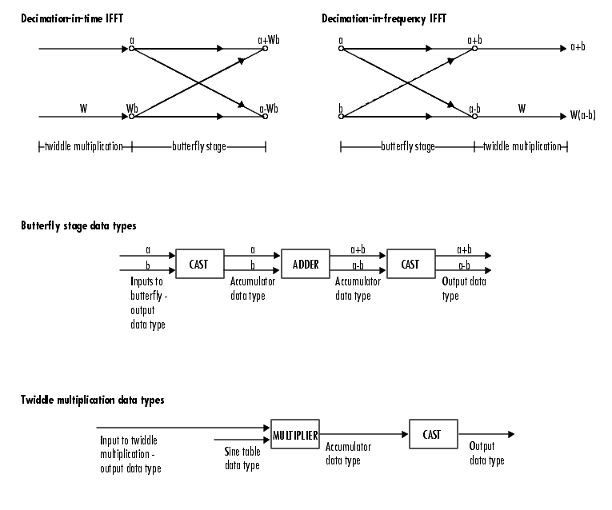
The output of the multiplier appears in the accumulator data type because both of the inputs to the multiplier are complex. For details on the complex multiplication performed, see Multiplication Data Types.

Note

When the block input is fixed point, all internal data types are signed fixed point.

Documentation

FFT

Description

Ports

Input

Port_1 — Input signal vector | matrix | N-D array

Output

Port_1 — FFT of input vector | matrix | N-D array

Parameters

Main

FFT implementation — FFT implementation Auto (default) | Radix-2 | FFTW

Output in bit-reversed order — Output in bit-reversed order off (default) | on

Dependencies

Divide output by FFT length — Divide output by FFT length off (default) | on

Inherit FFT length from input dimensions — Inherit FFT length from input dimensions on (default) | off

Dependencies

FFT length — FFT length 64 (default) | integer

Dependencies

Wrap input data when FFT length is shorter than input length — Wrap or truncate input on (default) | off

Dependencies

Data Types

Rounding mode — Rounding method Floor (default) | Ceiling | Convergent | Nearest | Round | Simplest | Zero

Limitations

Saturate on integer overflow — Saturate on integer overflow off (default) | on

Limitations

Sine table — Data type of sine table values Inherit: Same word length as input (default) | fixdt(1,16)

Limitations

Product output — Product output data type Inherit: Inherit via internal rule (default) | Inherit: Same as input | fixdt(1,16,0)

Accumulator — Accumulator data type Inherit: Inherit via internal rule (default) | Inherit: Same as input | Inherit: Same as product output | fixdt(1,16,0)

Output — Output data type Inherit: Inherit via internal rule (default) | Inherit: Same as input | fixdt(1,16,0)

Output Minimum — Minimum value block should output [] (default) | scalar

Output Maximum — Maximum value block should output [] (default) | scalar

Lock data type settings against changes by the fixed-point tools — Prevent fixed-point tools from overriding data types off (default) | on

Model Examples

Transform Time-Domain Data into Frequency Domain

Block Characteristics

Algorithms

FFTW Implementation

Radix-2 Implementation

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Fixed-Point Conversion Design and simulate fixed-point systems using Fixed-Point Designer™.

See Also

Objects

Functions

Blocks

Topics

DSP System Toolbox Documentation

Support

`Port_1` — Input signal
vector | matrix | N-D array

`Port_1` — FFT of input
vector | matrix | N-D array

`FFT implementation` — FFT implementation
`Auto` (default) | `Radix-2` | `FFTW`

`Output in bit-reversed order` — Output in bit-reversed order
`off` (default) | `on`

`Divide output by FFT length` — Divide output by FFT length
`off` (default) | `on`

`Inherit FFT length from input dimensions` — Inherit FFT length from input dimensions
`on` (default) | `off`

`FFT length` — FFT length
`64` (default) | integer

`Wrap input data when FFT length is shorter than input length` — Wrap or truncate input
`on` (default) | `off`

`Rounding mode` — Rounding method
`Floor` (default) | `Ceiling` | `Convergent` | `Nearest` | `Round` | `Simplest` | `Zero`

`Saturate on integer overflow` — Saturate on integer overflow
`off` (default) | `on`

`Sine table` — Data type of sine table values
`Inherit: Same word length as input` (default) | `fixdt(1,16)`

`Product output` — Product output data type
`Inherit: Inherit via internal rule` (default) | `Inherit: Same as input` | `fixdt(1,16,0)`

`Accumulator` — Accumulator data type
`Inherit: Inherit via internal rule` (default) | `Inherit: Same as input` | `Inherit: Same as product output` | `fixdt(1,16,0)`

`Output` — Output data type
`Inherit: Inherit via internal rule` (default) | `Inherit: Same as input` | `fixdt(1,16,0)`

`Output Minimum` — Minimum value block should output
`[]` (default) | scalar

`Output Maximum` — Maximum value block should output
`[]` (default) | scalar

`Lock data type settings against changes by the fixed-point tools` — Prevent fixed-point tools from overriding data types
`off` (default) | `on`

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Fixed-Point Conversion
Design and simulate fixed-point systems using Fixed-Point Designer™.