Graphical Representation of Trees

Introduction

You can use the function treeviewer to display a graphical representation of a tree, allowing you to examine interactively the prices and rates on the nodes of the tree until maturity. To get started with this process, first load the data file deriv.mat included in this toolbox.

load deriv.mat

Note

treeviewer price tree diagrams follow the convention that increasing prices appear on the upper branch of a tree and, consequently, decreasing prices appear on the lower branch. Conversely, for interest rate displays, decreasing interest rates appear on the upper branch (prices are rising) and increasing interest rates on the lower branch (prices are falling).

For information on the use of treeviewer to observe interest rate movement, see Observing Interest Rates. For information on using treeviewer to observe the movement of prices, see Observing Instrument Prices.

Observing Interest Rates

If you provide the name of an interest rate tree to the treeviewer function, it displays a graphical view of the path of interest rates. For example, here is the treeviewer representation of all the rates along both the up and down branches of HJMTree.

treeviewer(HJMTree)

The example in Isolating a Specific Node used bushpath to find the path of forward rates along an HJM tree by taking the first branch up and then two branches down the rate tree.

FRates = bushpath(HJMTree.FwdTree, [1 2 2])

FRates =

    1.0356
    1.0364
    1.0526
    1.0674

With the treeviewer function you can display the identical information by clicking along the same sequence of nodes, as shown next.

Next is a treeviewer representation of interest rates along several branches of BDTTree.

treeviewer(BDTTree)

Note

When using treeviewer with recombining trees, such as BDT, BK, and HW, you must click each node in succession from the beginning to the end. Because these trees can recombine, treeviewer is unable to complete the path automatically.

The example in Isolating a Specific Node used treepath to find the path of interest rates taking the first branch up and then two branches down the rate tree.

FRates = treepath(BDTTree.FwdTree, [1 2 2])

FRates =

    1.1000
    1.0979
    1.1377
    1.1606

You can display the identical information by clicking along the same sequence of nodes, as shown next.

Observing Instrument Prices

To use treeviewer to display a tree of instrument prices, provide the name of an instrument set along with the name of a price tree in your call to treeviewer, for example:

load deriv.mat
[Price, PriceTree] = hjmprice(HJMTree, HJMInstSet);
treeviewer(PriceTree, HJMInstSet)

With treeviewer you select each instrument individually in the instrument portfolio for display.

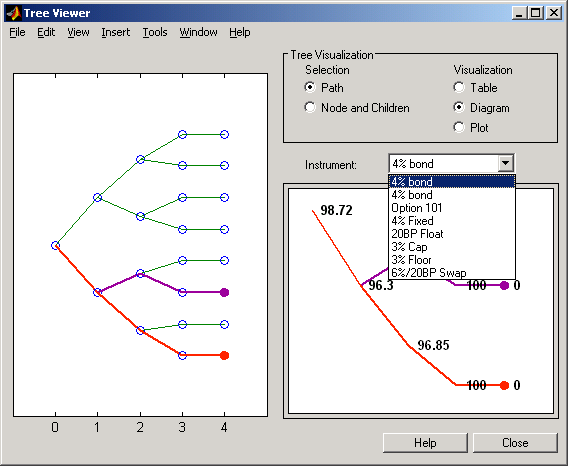
You can use an analogous process to view instrument prices based on the BDT interest rate tree included in deriv.mat.

load deriv.mat
[BDTPrice, BDTPriceTree] = bdtprice(BDTTree, BDTInstSet);
treeviewer(BDTPriceTree, BDTInstSet)

Valuation Date Prices

You can use treeviewer instrument-by-instrument to observe instrument prices through time. For the first 4% bond in the HJM instrument portfolio, treeviewer indicates a valuation date price of 98.72, the same value obtained by accessing the PriceTree structure directly.

As a further example, look at the sixth instrument in the price vector, the 3% cap. At the valuation date, its value obtained directly from the structure is 6.2831. Use treeviewer on this instrument to confirm this price.

Additional Observation Times

The second node represents the first-rate observation time, tObs = 1. This node displays two states, one representing the branch going up and the other one representing the branch going down.

Examine the prices of the node corresponding to the up branch.

PriceTree.PBush{2}(:,:,1)

As before, you can use treeviewer, this time to examine the price for the 4% bond on the up branch. treeviewer displays a price of 100.2 for the first node of the up branch, as expected.

Now examine the corresponding down branch.

PriceTree.PBush{2}(:,:,2)

Use treeviewer once again, now to observe the price of the 4% bond on the down branch. The displayed price of 96.3 conforms to the price obtained from direct access of the PriceTree structure. You may continue this process as far along the price tree as you want.

Documentation