rlevinson
Reverse Levinson-Durbin recursion
Syntax
r = rlevinson(a,efinal)
[r,u] = rlevinson(a,efinal)
[r,u,k] = rlevinson(a,efinal)
[r,u,k,e] = rlevinson(a,efinal)
Description
The reverse Levinson-Durbin recursion implements the step-down algorithm for solving the following symmetric Toeplitz system of linear equations for r, where r = [r(1) … r(p + 1)] and r(i)* denotes the complex conjugate of r(i).
r = rlevinson(a,efinal) solves the above
system of equations for r given vector a, where a = [1 a(2) … a(p + 1)]. In linear prediction applications, r represents
the autocorrelation sequence of the input to the prediction error filter, where r(1) is the zero-lag element. The figure below shows the typical filter of
this type, where H(z) is the optimal linear predictor,
x(n) is the input signal, is the predicted signal, and
e(n) is the prediction error.
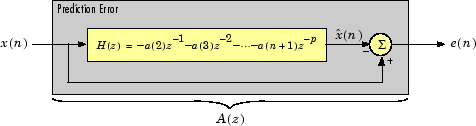
Input vector a represents the polynomial coefficients of this prediction error filter in descending powers of z.
The filter must be minimum-phase to generate a valid autocorrelation sequence.
efinal is the scalar prediction error power, which is equal to
the variance of the prediction error signal,
σ2(e).
[r,u] = rlevinson(a,efinal) returns upper
triangular matrix U from the UDU* decomposition
where
and E is a diagonal matrix with elements returned in output
e (see below). This decomposition permits the efficient
evaluation of the inverse of the autocorrelation matrix,
R−1.
Output matrix u contains the prediction filter polynomial,
a, from each iteration of the reverse Levinson-Durbin
recursion
where ai(j) is the jth coefficient of the ith order prediction filter polynomial (i.e., step i in the recursion). For example, the 5th order prediction filter polynomial is
a5 = u(5:-1:1,5)'
Note that u(p+1:-1:1,p+1)' is the input polynomial coefficient
vector a.
[r,u,k] = rlevinson(a,efinal)
returns a vector k of length p + 1
containing the reflection coefficients. The reflection coefficients are the conjugates
of the values in the first row of u.
k = conj(u(1,2:end))
[r,u,k,e] = rlevinson(a,efinal) returns a
vector of length p + 1 containing the prediction errors
from each iteration of the reverse Levinson-Durbin recursion: e(1) is
the prediction error from the first-order model, e(2) is the
prediction error from the second-order model, and so on.
These prediction error values form the diagonal of the matrix E in the UDU* decomposition of R−1.
Examples
Optimum Autoregressive Model Order
Estimate the spectrum of two sine waves in noise using an autoregressive model. Choose the best model order from a group of models returned by the reverse Levinson-Durbin recursion.
Generate the signal. Specify a sample rate of 1 kHz and a signal duration of 50 seconds. The sinusoids have frequencies of 50 Hz and 55 Hz. The noise has a variance of 0.2².
Fs = 1000; t = (0:50e3-1)'/Fs; x = sin(2*pi*50*t) + sin(2*pi*55*t) + 0.2*randn(50e3,1);
Estimate the autoregressive model parameters.
[a,e] = arcov(x,100); [r,u,k] = rlevinson(a,e);
Estimate the power spectral density for orders 1, 5, 25, 50, and 100.
N = [1 5 25 50 100]; nFFT = 8096; P = zeros(nFFT,5); for idx = 1:numel(N) order = N(idx); ARtest = flipud(u(:,order)); P(:,idx) = 1./abs(fft(ARtest,nFFT)).^2; end
Plot the PSD estimates.
F = (0:1/nFFT:1/2-1/nFFT)*Fs; plot(F, 10*log10(P(1:length(P)/2,:))) grid legend([repmat('Order = ',[5 1]) num2str(N')]) xlabel('Frequency (Hz)') ylabel('dB') xlim([35 70])
References
[1] Kay, Steven M. Modern Spectral Estimation: Theory and Application. Englewood Cliffs, NJ: Prentice-Hall, 1988.