inv

Invert models

Syntax

inv

Description

inv inverts the input/output relation

y=G(s)u

to produce the model with the transfer matrix H(s)=G(s)−1.

u=H(s)y

This operation is defined only for square systems (same number of inputs and outputs) with an invertible feedthrough matrix D. inv handles both continuous- and discrete-time systems.

Examples

Consider

H(s)=[11s+101]

At the MATLAB® prompt, type

H = [1 tf(1,[1 1]);0 1]
Hi = inv(H)

to invert it. These commands produce the following result.

Transfer function from input 1 to output...
 #1:  1
 
 #2:  0
 
Transfer function from input 2 to output...
       -1
 #1:  -----
      s + 1
 
 #2:  1

You can verify that

H * Hi

is the identity transfer function (static gain I).

Limitations

Do not use inv to model feedback connections such as

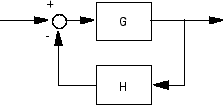
While it seems reasonable to evaluate the corresponding closed-loop transfer function (I+GH)−1G as

inv(1+g*h) * g

this typically leads to nonminimal closed-loop models. For example, 

g = zpk([],1,1)
h = tf([2 1],[1 0])
cloop = inv(1+g*h) * g

yields a third-order closed-loop model with an unstable pole-zero cancellation at s = 1.

cloop

Zero/pole/gain:
      s (s-1)
-------------------
(s-1) (s^2 + s + 1)

Use feedback to avoid such pitfalls.

cloop = feedback(g,h)

Zero/pole/gain:
      s
-------------
(s^2 + s + 1)
Introduced before R2006a

Control System Toolbox Documentation

Support