SISO Feedback Loop

Create an aggregate model of the following block diagram from r to y.

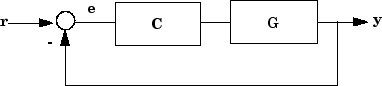
Create C and G, and name the inputs and outputs.

C = pid(2,1); 
C.u = 'e';  
C.y = 'u';
G = zpk([],[-1,-1],1);
G.u = 'u';  
G.y = 'y';

The notations C.u and C.y are shorthand expressions equivalent to C.InputName and C.OutputName, respectively. For example, entering C.u = 'e' is equivalent to entering C.InputName = 'e'. The command sets the InputName property of C to the value 'e'.

Create the summing junction.

Sum = sumblk('e = r - y');

Combine C, G, and the summing junction to create the aggregate model from r to y.

T = connect(G,C,Sum,'r','y');

connect automatically joins inputs and outputs with matching names.

MIMO Feedback Loop

Create the control system of the previous example where G and C are both 2-input, 2-output models.

C = [pid(2,1),0;0,pid(5,6)];
C.InputName = 'e';  
C.OutputName = 'u';
G = ss(-1,[1,2],[1;-1],0);
G.InputName = 'u';  
G.OutputName = 'y';

When you specify single names for vector-valued signals, the software automatically performs vector expansion of the signal names. For example, examine the names of the inputs to C.

C.InputName

ans = 

    'e(1)'
    'e(2)'

Create a 2-input, 2-output summing junction.

Sum = sumblk('e = r-y',2);

sumblk also performs vector expansion of the signal names.

Interconnect the models to obtain the closed-loop system.

T = connect(G,C,Sum,'r','y');

The block diagram elements G, C, and Sum are all 2-input, 2-output models. Therefore, connect performs the same vector expansion. connect selects all entries of the two-input signals 'r' and 'y' as inputs and outputs to T, respectively. For example, examine the input names of T.

T.InputName

ans = 

    'r(1)'
    'r(2)'

Feedback Loop With Analysis Point Inserted by connect

Create a model of the following block diagram from r to y. Insert an analysis point at an internal location, u.

Create C and G, and name the inputs and outputs.

C = pid(2,1); 
C.InputName = 'e';  
C.OutputName = 'u';
G = zpk([],[-1,-1],1);
G.InputName = 'u';  
G.OutputName = 'y';

Create the summing junction.

Sum = sumblk('e = r - y');

Combine C, G, and the summing junction to create the aggregate model, with an analysis point at u.

T = connect(G,C,Sum,'r','y','u')

T =

  Generalized continuous-time state-space model with 1 outputs, 1 inputs, 3 states, and the following blocks:
    AnalysisPoints_: Analysis point, 1 channels, 1 occurrences.

Type "ss(T)" to see the current value, "get(T)" to see all properties, and "T.Blocks" to interact with the blocks.

The resulting T is a genss model. The connect command creates the AnalysisPoint block, AnalysisPoints_, and inserts it into T. To see the name of the analysis point channel in AnalysisPoints_, use getPoints.

getPoints(T)

ans = 1x1 cell array
    {'u'}

The analysis point channel is named 'u'. You can use this analysis point to extract system responses. For example, the following commands extract the open-loop transfer at u and the closed-loop response at y to a disturbance injected at u.

L = getLoopTransfer(T,'u',-1);
Tuy = getIOTransfer(T,'u','y');

T is equivalent to the following block diagram, where AP_u designates the AnalysisPoint block AnalysisPoints_ with channel name u.

Index-Based Interconnection

Create an aggregate model of the following block diagram from r to y using index-based interconnection.

Create C, G, and the unconnected aggregate model blksys.

C = pid(2,1); 
G = zpk([],[-1,-1],1);
blksys = append(C,G);

The inputs u(1),u(2) of blksys correspond to the inputs of C and G, respectively. The outputs w(1),w(2) of blksys correspond to the outputs of C and G, respectively.

Create the matrix connections, which specifies which outputs of blksys connect to which inputs of blksys.

connections = [2 1; 1 -2];

The first row indicates that w(1) connects to u(2); in other words, that the output of C connects to the input of G. The second row indicates that -w(2) connects to u(1); in other words, that the negative of the output of G connects to the input of C.

Create the connected aggregate model from r to y.

T = connect(blksys,connections,1,2)

The last two arguments specify the external inputs and outputs in terms of the indices of blksys. The argument 1 specifies that the external input connects to u(1). The last argument, 2, specifies that the external output connects from w(2).