Deploy Shallow Neural Network Simulink Diagrams
The function gensim generates block
descriptions of networks so you can simulate them using Simulink® software.
gensim(net,st)
The second argument to gensim determines the sample time, which
is normally chosen to be some positive real value.
If a network has no delays associated with its input weights or layer weights,
this value can be set to -1. A value of -1 causes gensim to
generate a network with continuous sampling.
Example
Here is a simple problem defining a set of inputs p and
corresponding targets t.
p = [1 2 3 4 5]; t = [1 3 5 7 9];
The code below designs a linear layer to solve this problem.
net = newlind(p,t)
You can test the network on your original inputs with
sim.
y = sim(net,p)
The results show the network has solved the problem.
y =
1.0000 3.0000 5.0000 7.0000 9.0000
Call gensim as follows to generate a Simulink version of the network.
gensim(net,-1)
The second argument is -1, so the resulting network block samples continuously.
The call to gensim opens the following Simulink Editor, showing a system consisting of the linear network
connected to a sample input and a scope.
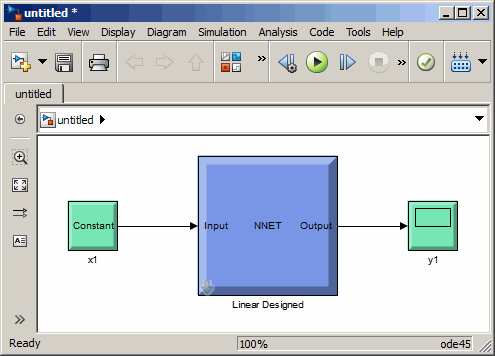
To test the network, double-click the input Constant x1
block on the left.
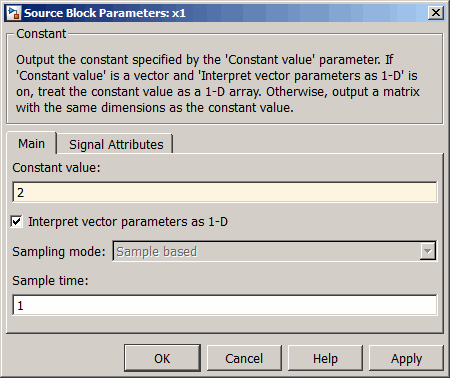
The input block is actually a standard Constant block. Change the constant
value from the initial randomly generated value to 2, and
then click OK.
Select the menu option Simulation > Run. Simulink takes a moment to simulate the system.
When the simulation is complete, double-click the output
y1 block on the right to see the following display
of the network’s response.
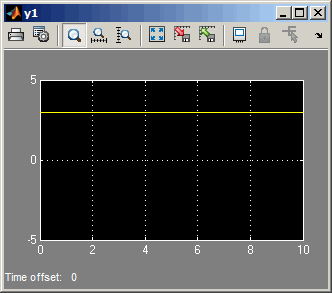
Note that the output is 3, which is the correct output for an input of 2.
Suggested Exercises
Here are a couple exercises you can try.
Change the Input Signal
Replace the constant input block with a signal generator from the standard Simulink Sources blockset. Simulate the system and view the network’s response.
Use a Discrete Sample Time
Recreate the network, but with a discrete sample time of 0.5, instead of continuous sampling.
gensim(net,0.5)
Again, replace the constant input with a signal generator. Simulate the system and view the network’s response.
Generate Functions and Objects
For information on simulating and deploying shallow neural networks with MATLAB® functions, see Deploy Shallow Neural Network Functions.