graphpred2path

Convert predecessor indices to paths

Syntax

path = graphpred2path(pred, D)

Arguments

pred Row vector or matrix of predecessor node indices. The value of the root (or source) node in pred must be 0.
DDestination node in pred.

Description

Tip

For introductory information on graph theory functions, see Graph Theory Functions.

path = graphpred2path(pred, D) traces back a path by following the predecessor list in pred starting at destination node D.

The value of the root (or source) node in pred must be 0. If a NaN is found when following the predecessor nodes, graphpred2path returns an empty path.

If pred is a ...And D is a ...Then path is a ...
row vector of predecessor node indicesscalarrow vector listing the nodes from the root (or source) to D.
row vectorrow cell array with every column containing the path to the destination for every element in D.
matrixscalarcolumn cell array with every row containing the path for every row in pred.
row vectormatrix cell array with every row containing the paths for the respective row in pred, and every column containing the paths to the respective destination in D.

Note

If D is omitted, the paths to all the destinations are calculated for every predecessor listed in pred.

Examples

  1. Create a phytree object from the phylogenetic tree file for the GLR_HUMAN protein.

    tr = phytreeread('pf00002.tree')
    Phylogenetic tree object with 33 leaves (32 branches)

  2. View the phytree object.

    view(tr)

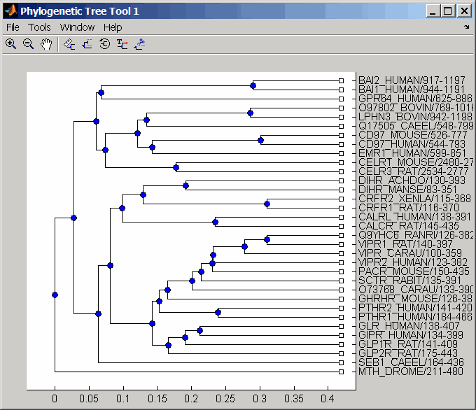
  3. From the phytree object, create a connection matrix to represent the phylogenetic tree. 

    [CM,labels,dist] = getmatrix(tr);

  4. Find the nodes from the root to one leaf in the phylogenetic tree created from the phylogenetic tree file for the GLR_HUMAN protein.

    root_loc = size(CM,1)

root_loc =

    65

 glr_loc = strncmp('GLR',labels,3);
 glr_loc_ind = find(glr_loc)

glr_loc_ind =

    12

[T,PRED]=graphminspantree(CM,root_loc);
PATH = graphpred2path(PRED,glr_loc_ind)

PATH =

    65    64    53    52    46    45    44    43    12

References

[1] Siek, J.G., Lee, L-Q, and Lumsdaine, A. (2002). The Boost Graph Library User Guide and Reference Manual, (Upper Saddle River, NJ:Pearson Education).

See Also

| | | | | | | | |

Introduced in R2006b

Bioinformatics Toolbox Documentation

Support