kaiserord

Signal Processing Toolbox

Estimate parameters for fir1 with Kaiser window.

[n,Wn,beta,ftype] = kaiserord(f,a,dev)
[n,Wn,beta,ftype] = kaiserord(f,a,dev,Fs)
c = kaiserord(f,a,dev,Fs,'cell')

Description

kaiserord returns a filter order n and beta parameter to specify a Kaiser window for use with the fir1 function. Given a set of specifications in the frequency domain, kaiserord estimates the minimum FIR filter order that will approximately meet the specifications. kaiserord converts the given filter specifications into passband and stopband ripples and converts cutoff frequencies into the form needed for windowed FIR filter design.

NOTE
If the band ripples are specified as unequal, the smallest one is used, since the Kaiser window method is constrained to give filters with equal ripple heights in all the passbands and stopbands.

[n,Wn,beta,ftype] = kaiserord(f,a,dev)

finds the approximate order n, normalized frequency band edges Wn, and weights that meet input specifications f, a, and dev. f is a vector of band edges and a is a vector specifying the desired amplitude on the bands defined by f. The length of f is twice the length of a, minus 2. Together, f and a define a desired piecewise constant response function. dev is a vector the same size as a that specifies the maximum allowable error or deviation between the frequency response of the output filter and its desired amplitude, for each band.

fir1 can use the resulting order n, frequency vector Wn, multiband magnitude type ftype, and the Kaiser window parameter beta. The ftype string is intended for use with fir1; it is equal to 'high' for a highpass filter and 'stop' for a bandstop filter. For multiband filters, it can be equal to 'dc-0' when the first band is a stopband (starting at f = 0) or 'dc-1' when the first band is a passband.

To design a filter b that approximately meets the specifications given by kaiser parameters f, a, and dev:

b = fir1(n,Wn,kaiser(n+1,beta),ftype,'noscale')

[n,Wn,beta,ftype] = kaiserord(f,a,dev,Fs)

specifies a sampling frequency Fs. If not present, Fs defaults to 2 Hz, implying a Nyquist frequency of 1 Hz. You can therefore specify band edges scaled to a particular application's sampling frequency.

c = kaiserord(f,a,dev,Fs,'cell')

is a cell-array whose elements are the parameters to fir1.

NOTE
In some cases, kaiserord underestimates or overestimates the order n. If the filter does not meet the specifications, try a higher order such as n+1, n+2, and so on, or a lower order.

NOTE
Results are inaccurate if the cutoff frequencies are near 0 or the Nyquist frequency or if dev is large (greater than 10%).

Algorithm

kaiserord uses empirically derived formulas for estimating the orders of lowpass filters, as well as differentiators and Hilbert transformers. Estimates for multiband filters (such as bandpass filters) are derived from the lowpass design formulas.

The design formulas that underlie the Kaiser window and its application to FIR filter design are

where

= -20log₁₀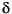

is the stopband attenuation expressed in decibels (recall that

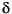_p =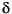

_s is required). The design formula is:

where n is the filter order.

Examples

Design a lowpass filter with passband from 0 to 1 kHz and stopband from 1500 Hz to 4 kHz. Specify passband ripple of 5% and stopband attenuation of 40 dB:

fsamp = 8000;
fcuts = [1000 1500];
mags = [1 0];
devs = [0.05 0.01];
[n,Wn,beta,ftype] = kaiserord(fcuts,mags,devs,fsamp);
hh = fir1(n,Wn,ftype,kaiser(n+1,beta),'noscale');
freqz(hh)

Design an odd-length bandpass filter (note that odd length means even order, so the input to fir1 must be an even integer):

fsamp = 8000;
fcuts = [1000 1300 2410];
mags = [0 1 0];
devs = [0.01 0.05 0.01];
[n,Wn,beta,ftype] = kaiserord(fcuts,mags,devs,fsamp);
n = n + rem(n,2);
hh = fir1(n,Wn,ftype,kaiser(n+1,beta),'noscale');
[H,f] = freqz(hh,1,1024,fsamp);
plot(f,abs(H)),grid on

Design a lowpass filter with a passband cutoff of 1500 Hz, a stopband cutoff of 2000 Hz, passband ripple of 0.01, stopband ripple of 0.1, and a sampling frequency of 8000 Hz:

[n,Wn,beta,ftype] = kaiserord([1500 2000],[1 0],[0.01 0.1],8000);
b = fir1(n,Wn,ftype,kaiser(n+1,beta),'noscale');

This is equivalent to

c = kaiserord([1500 2000],[1 0],[0.01 0.1],8000,'cell');
b = fir1(c{:});

Remarks

Be careful to distinguish between the meanings of filter length and filter order. The filter length is the number of impulse response samples in the FIR filter. Generally, the impulse response is indexed from n = 0 to n = L-1, where L is the filter length. The filter order is the highest power in a z-transform representation of the filter. For an FIR transfer function, this representation is a polynomial in z, where the highest power is z^L-1 and the lowest power is z⁰. The filter order is 1 less than the length (L-1) and is also equal to the number of zeros of the z polynomial.

Diagnostics

The lengths of the frequency, magnitude, and deviation vectors must match; otherwise, kaiserord gives the following error message:

Requires M and DEV to be the same length.
Length of F must be 2*length(M)-2.

When magnitudes are not specified correctly, kaiserord gives the following error messages:

Stopbands must be zero.
All passbands must have the same height.

If the band edges are not strictly increasing, kaiserord gives the following error message:

Bandedges must be strictly increasing.

`fir1`	Window-based finite impulse response filter design-- standard response.
`kaiser`	Kaiser window.
`remezord`	Parks-McClellan optimal FIR filter order estimation.