dpss
Purpose
Discrete prolate spheroidal sequences (Slepian sequences).
Syntax
[e,v] = dpss(n,nw)
[e,v] = dpss(n,nw,'calc')
[e,v] = dpss(n,nw,'spline')
[e,v] = dpss(n,nw,'spline',Ni)
[e,v] = dpss(n,nw,'linear')
[e,v] = dpss(n,nw,'linear',Ni)
[e,v] = dpss(n,nw,'trace')
[e,v] = dpss(n,nw,'int','trace')
Description
[e,v] = dpss(n,nw)
generates the first 2*nw discrete prolate spheroidal sequences (DPSS) of length n, in the columns of e, and their corresponding concentrations in vector v. They are generated in the DPSS MAT-file database dpss.mat.
- The sequences are generated in the frequency band
|
| 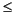
(2
W), where
W = nw/n is the half-bandwidth and  is in radians.
is in radians.
e(:,1) is the length n signal most concentrated in the frequency band
|
| 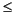
(2
W) radians, e(:,2) is the signal orthogonal to e(:,1) that is most concentrated in this band, e(:,3) is the signal orthogonal to both e(:,1) and e(:,2) that is most concentrated in this band, etc.
- For multitaper spectral analysis, typical choices for
nw are 2, 5/2, 3, 7/2, or 4.
If you specify only n and nw, DPSS follows these rules for selecting an efficient (although sometimes approximate) algorithm:
- If
n < 500, the sequences are calculated directly.
- If
n 
500,
- look for sequences in the DPSS MAT-file database
dpss.mat;
- if not found, linearly interpolate from sequences with the same
nw and
next largest n in the database;
- if not found, use spline interpolation from length 64 sequences.
[e,v] = dpss(n,nw,'calc')
forces DPSS to calculate e and v directly. This can take a long time for large n and nw.
[e,v] = dpss(n,nw,'spline')
uses spline interpolation to compute e and v from the sequences in dpss.mat with length closest to n.
[e,v] = dpss(n,nw,'spline',Ni)
interpolates from existing length Ni sequences.
[e,v] = dpss(n,nw,'linear')
and
[e,v] = dpss(n,nw,'linear',Ni)
use linear interpolation, which is much faster but less accurate than spline interpolation. 'linear' requires Ni > n.
[e,v] = dpss(n,nw,'trace')
and
[e,v] = dpss(n,nw,'int','trace')
use a trailing 'trace' argument to find out which method DPSS uses, where 'int' is either 'spline' or 'linear'.
See Also
References
[1] Percival, D.B., and A.T. Walden. Spectral Analysis for Physical Applications: Multitaper and Conventional Univariate Techniques. Cambridge: Cambridge University Press, 1993.
[ Previous | Help Desk | Next ]

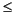

 is in radians.
is in radians.